Choose univariate class intervals
classIntervals.RdThe function provides a uniform interface to finding class intervals for continuous numerical variables, for example for choosing colours or symbols for plotting. Class intervals are non-overlapping, and the classes are left-closed — see findInterval. Argument values to the style chosen are passed through the dot arguments. classIntervals2shingle converts a classIntervals object into a shingle. Labels generated in methods are like those found in cut unless cutlabels=FALSE.
Usage
classIntervals(var, n, style = "quantile", rtimes = 3, ...,
intervalClosure = c("left", "right"), dataPrecision = NULL,
warnSmallN = TRUE, warnLargeN = TRUE, largeN = 3000L, samp_prop = 0.1,
gr = c("[", "]"))
# S3 method for class 'classIntervals'
plot(x, pal, ...)
# S3 method for class 'classIntervals'
print(x, digits = getOption("digits"), ...,
under="under", over="over", between="-", cutlabels=TRUE, unique=FALSE,big.mark=NULL)
nPartitions(x)
classIntervals2shingle(x)Arguments
- var
a continuous numerical variable
- n
number of classes required, if missing,
nclass.Sturgesis used; see also the "dpih" and "headtails" styles for automatic choice of the number of classes- style
chosen style: one of "fixed", "sd", "equal", "pretty", "quantile", "kmeans", "hclust", "bclust", "fisher", "jenks", "dpih", "headtails", "maximum", or "box"
- rtimes
number of replications of var to catenate and jitter; may be used with styles "kmeans" or "bclust" in case they have difficulties reaching a classification
- intervalClosure
default “left”, allows specification of whether partition intervals are closed on the left or the right (added by Richard Dunlap). Note that the sense of interval closure is hard-coded as “right”-closed when
style="jenks"(see Details below).- dataPrecision
default NULL, permits rounding of the interval endpoints (added by Richard Dunlap). The data precision used for printing interval values in the legend returned by
findColours, and in theprintmethod for classIntervals objects. If intervalClosure is “left”, the value returned isceilingof the data value multiplied by 10 to the dataPrecision power, divided by 10 to the dataPrecision power. The argument does not roundvar, the input variable.- warnSmallN
default TRUE, if FALSE, quietens warning for n >= nobs
- warnLargeN
default TRUE, if FALSE large data handling not used
- largeN
default 3000L, the QGIS sampling threshold; if
warnLargeNis TRUE and the number of observations is greater thanlargeN, the observations presented to "fisher" and "jenks" are either asamp_prop=sample of the observations, or a sample oflargeN, whichever is smaller- samp_prop
default 0.1, QGIS 10% sampling proportion
- gr
default
c("[", "]"), if the units package is available,units::units_options("group")may be used directly to give the enclosing bracket style- ...
arguments to be passed to the functions called in each style
- x
"classIntervals" object for printing, conversion to shingle, or plotting
- under
character string value for "under" in printed table labels if cutlabels=FALSE
- over
character string value for "over" in printed table labels if cutlabels=FALSE
- between
character string value for "between" in printed table labels if cutlabels=FALSE
- digits
minimal number of significant digits in printed table labels
- cutlabels
default TRUE, use cut-style labels in printed table labels
- unique
default FALSE; if TRUE, collapse labels of single-value classes
- big.mark
default NULL; an object of class
characterto specify to 'thousands' separator- pal
a character vector of at least two colour names for colour coding the class intervals in an ECDF plot;
colorRampPaletteis used internally to create the correct number of colours
Details
The "fixed" style permits a "classIntervals" object to be specified with given breaks, set in the fixedBreaks argument; the length of fixedBreaks should be n+1; this style can be used to insert rounded break values.
The "sd" style chooses breaks based on pretty of the centred and scaled variables, and may have a number of classes different from n; the returned par= includes the centre and scale values. If argument sd_m is given as a numeric vector of multiples to apply to the standard deviation such as c(-Inf, -2, -1, 0, 1, 2, +Inf)
The "equal" style divides the range of the variable into n parts.
The "pretty" style chooses a number of breaks not necessarily equal to n using pretty, but likely to be legible; arguments to pretty may be passed through ....
The "quantile" style provides quantile breaks; arguments to quantile may be passed through .... probs is never permitted, as it is set using the n argument to probs = seq(0, 1, 1/n).
The "kmeans" style uses kmeans to generate the breaks; it may be anchored using set.seed; the pars attribute returns the kmeans object generated; if kmeans fails, a jittered input vector containing rtimes replications of var is tried — with few unique values in var, this can prove necessary; arguments to kmeans may be passed through ....
The "hclust" style uses hclust to generate the breaks using hierarchical clustering; the pars attribute returns the hclust object generated, and can be used to find other breaks using getHclustClassIntervals; arguments to hclust may be passed through ....
The "bclust" style uses bclust to generate the breaks using bagged clustering; it may be anchored using set.seed; the pars attribute returns the bclust object generated, and can be used to find other breaks using getBclustClassIntervals; if bclust fails, a jittered input vector containing rtimes replications of var is tried — with few unique values in var, this can prove necessary; arguments to bclust may be passed through ....
The "fisher" style uses the algorithm proposed by W. D. Fisher (1958) and discussed by Slocum et al. (2005) as the Fisher-Jenks algorithm; added here thanks to Hisaji Ono. This style will subsample by default for more than 3000 observations. This style should always be preferred to "jenks" as it uses the original Fortran code and runs nested for-loops much faster.
The "jenks" style has been ported from Jenks' code, and has been checked for consistency with ArcView, ArcGIS, and MapInfo (with some remaining differences); added here thanks to Hisaji Ono (originally reported as Basic, now seen as Fortran (as described in a talk last seen at http://www.irlogi.ie/wp-content/uploads/2016/11/NUIM_ChoroHarmful.pdf, slides 26-27)). Note that the sense of interval closure is reversed from the other styles, and in this implementation has to be right-closed - use cutlabels=TRUE in findColours on the object returned to show the closure clearly, and use findCols to extract the classes for each value. This style will subsample by default for more than 3000 observations.
The "dpih" style uses the dpih() function from KernSmooth (Wand, 1995) implementing direct plug-in methodology to select the bin width of a histogram.
The "headtails" style uses the algorithm proposed by Bin Jiang (2013), in order to find groupings or hierarchy for data with a heavy-tailed distribution. This classification scheme partitions all of the data values around the mean into two parts and continues the process iteratively for the values (above the mean) in the head until the head part values are no longer heavy-tailed distributed. Thus, the number of classes and the class intervals are both naturally determined. By default the algorithm uses thr = 0.4, meaning that when the head represents more than 40% of the observations the distribution is not considered heavy-tailed. The threshold argument thr may be modified through ... (see Examples).
The "maximum" style uses the Maximum Breaks method of classification finding the k - 1 largest differences in var. The mean of the values that generated the largest splits is used as the interval boundary.
The "box" style generates 7 breaks (therefore 6 categories) based on a box-and-whisker plot. First and last categories include the data values considered as outliers, and the four remaining categories are defined by the percentiles 25, 50 and 75 of the data distribution. By default, the identification of outliers is based on the interquantile range (IQR), so values lower than percentile 25 - 1.5 * IQR or higher than percentile 75 + 1.5 * IQR are considered as outliers. The multiplier applied to the IQR iqr_mult = 1.5 may be modified through ...; the value must not be negative. As in the "quantile" style, the type= argument may be used to choose the quantile algoritm (default 7, standard boxplots use 5 or 2). From 0.4-9 and #41, the maximum and minimum are set to +Inf and -Inf to avoid errors induced in the earlier version where breaks could cease to be strictly ascending. The legacy= argument with value TRUE may be used to revert to the previous behaviour.
Value
an object of class "classIntervals":
- var
the input variable
- brks
a vector of breaks
and attributes:
- style
the style used
- parameters
parameter values used in finding breaks
- nobs
number of different finite values in the input variable
- call
this function's call
- intervalClosure
string, whether closure is “left” or “right”
- dataPrecision
the data precision used for printing interval values in the legend returned by
findColours, and in theprintmethod for classIntervals objects. If intervalClosure is “left”, the value returned isceilingof the data value multiplied by 10 to the dataPrecision power, divided by 10 to the dataPrecision power.
References
Armstrong, M. P., Xiao, N., Bennett, D. A., 2003. "Using genetic algorithms to create multicriteria class intervals for choropleth maps". Annals, Association of American Geographers, 93 (3), 595–623;
Jenks, G. F., Caspall, F. C., 1971. "Error on choroplethic maps: definition, measurement, reduction". Annals, Association of American Geographers, 61 (2), 217–244;
Dent, B. D., 1999, Cartography: thematic map design. McGraw-Hill, Boston, 417 pp.;
Slocum TA, McMaster RB, Kessler FC, Howard HH 2005 Thematic Cartography and Geographic Visualization, Prentice Hall, Upper Saddle River NJ.;
Fisher, W. D. 1958 "On grouping for maximum homogeneity", Journal of the American Statistical Association, 53, pp. 789–798 (https://lib.stat.cmu.edu/cmlib/src/cluster/fish.f)
Wand, M. P. 1995. Data-based choice of histogram binwidth. The American Statistician, 51, 59-64.
Jiang, B. 2013 "Head/tail breaks: A new classification scheme for data with a heavy-tailed distribution", The Professional Geographer, 65 (3), 482 – 494. (https://arxiv.org/abs/1209.2801v1)
Note
From version 0.1-11, the default representation has been changed to use cutlabels=TRUE, and representation within intervals has been corrected, thanks to Richard Dunlap. From version 0.1-15, the print method drops the calculation of the possible number of combinations of observations into classes, which generated warnings for n > 170.
See also
findColours, findCols, pretty, quantile, kmeans, hclust, bclust, findInterval, colorRamp, nclass, shingle
Examples
if (!require("spData", quietly=TRUE)) {
message("spData package needed for examples")
run <- FALSE
} else {
run <- TRUE
}
if (run) {
data(jenks71, package="spData")
pal1 <- c("wheat1", "red3")
opar <- par(mfrow=c(2,3))
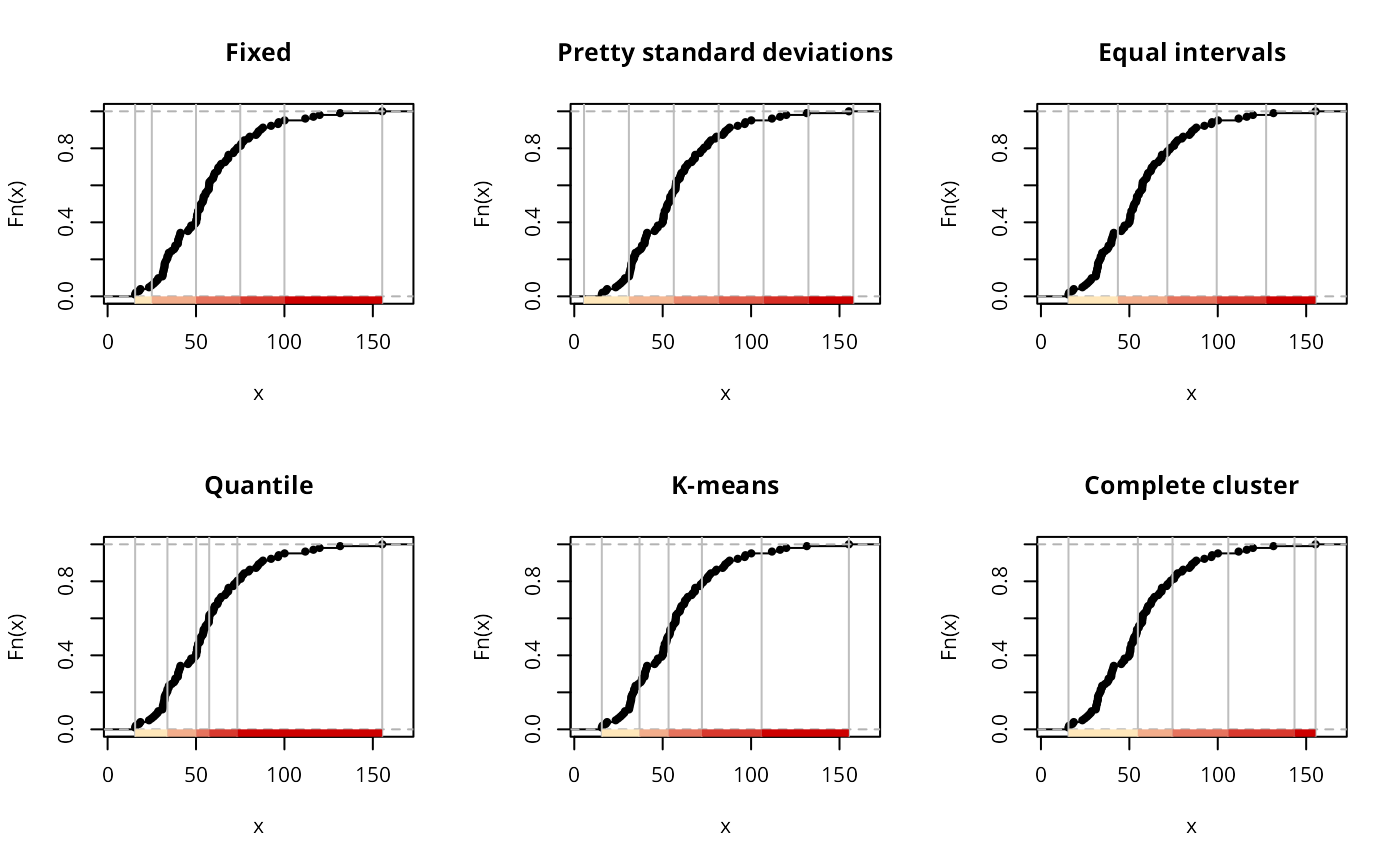
plot(classIntervals(jenks71$jenks71, n=5, style="fixed",
fixedBreaks=c(15.57, 25, 50, 75, 100, 155.30)), pal=pal1, main="Fixed")
plot(classIntervals(jenks71$jenks71, n=5, style="sd"), pal=pal1, main="Pretty standard deviations")
plot(classIntervals(jenks71$jenks71, n=5, style="equal"), pal=pal1, main="Equal intervals")
plot(classIntervals(jenks71$jenks71, n=5, style="quantile"), pal=pal1, main="Quantile")
set.seed(1)
plot(classIntervals(jenks71$jenks71, n=5, style="kmeans"), pal=pal1, main="K-means")
plot(classIntervals(jenks71$jenks71, n=5, style="hclust", method="complete"),
pal=pal1, main="Complete cluster")
}
 if (run) {
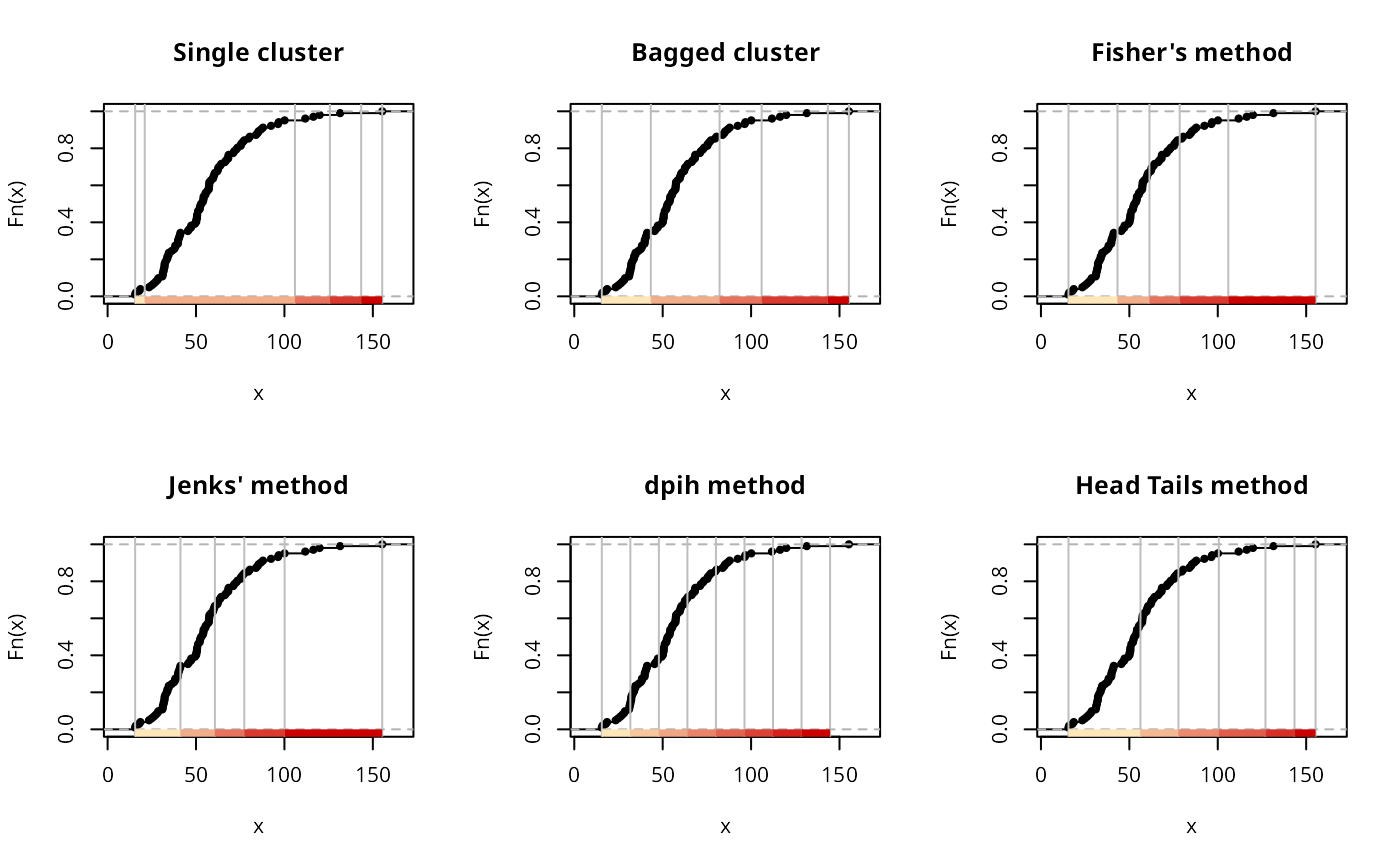
plot(classIntervals(jenks71$jenks71, n=5, style="hclust", method="single"),
pal=pal1, main="Single cluster")
set.seed(1)
plot(classIntervals(jenks71$jenks71, n=5, style="bclust", verbose=FALSE),
pal=pal1, main="Bagged cluster")
plot(classIntervals(jenks71$jenks71, n=5, style="fisher"), pal=pal1,
main="Fisher's method")
plot(classIntervals(jenks71$jenks71, n=5, style="jenks"), pal=pal1,
main="Jenks' method")
plot(classIntervals(jenks71$jenks71, style="dpih"), pal=pal1,
main="dpih method")
plot(classIntervals(jenks71$jenks71, style="headtails", thr = 1), pal=pal1,
main="Head Tails method")
}
if (run) {
plot(classIntervals(jenks71$jenks71, n=5, style="hclust", method="single"),
pal=pal1, main="Single cluster")
set.seed(1)
plot(classIntervals(jenks71$jenks71, n=5, style="bclust", verbose=FALSE),
pal=pal1, main="Bagged cluster")
plot(classIntervals(jenks71$jenks71, n=5, style="fisher"), pal=pal1,
main="Fisher's method")
plot(classIntervals(jenks71$jenks71, n=5, style="jenks"), pal=pal1,
main="Jenks' method")
plot(classIntervals(jenks71$jenks71, style="dpih"), pal=pal1,
main="dpih method")
plot(classIntervals(jenks71$jenks71, style="headtails", thr = 1), pal=pal1,
main="Head Tails method")
}
 if (run) {
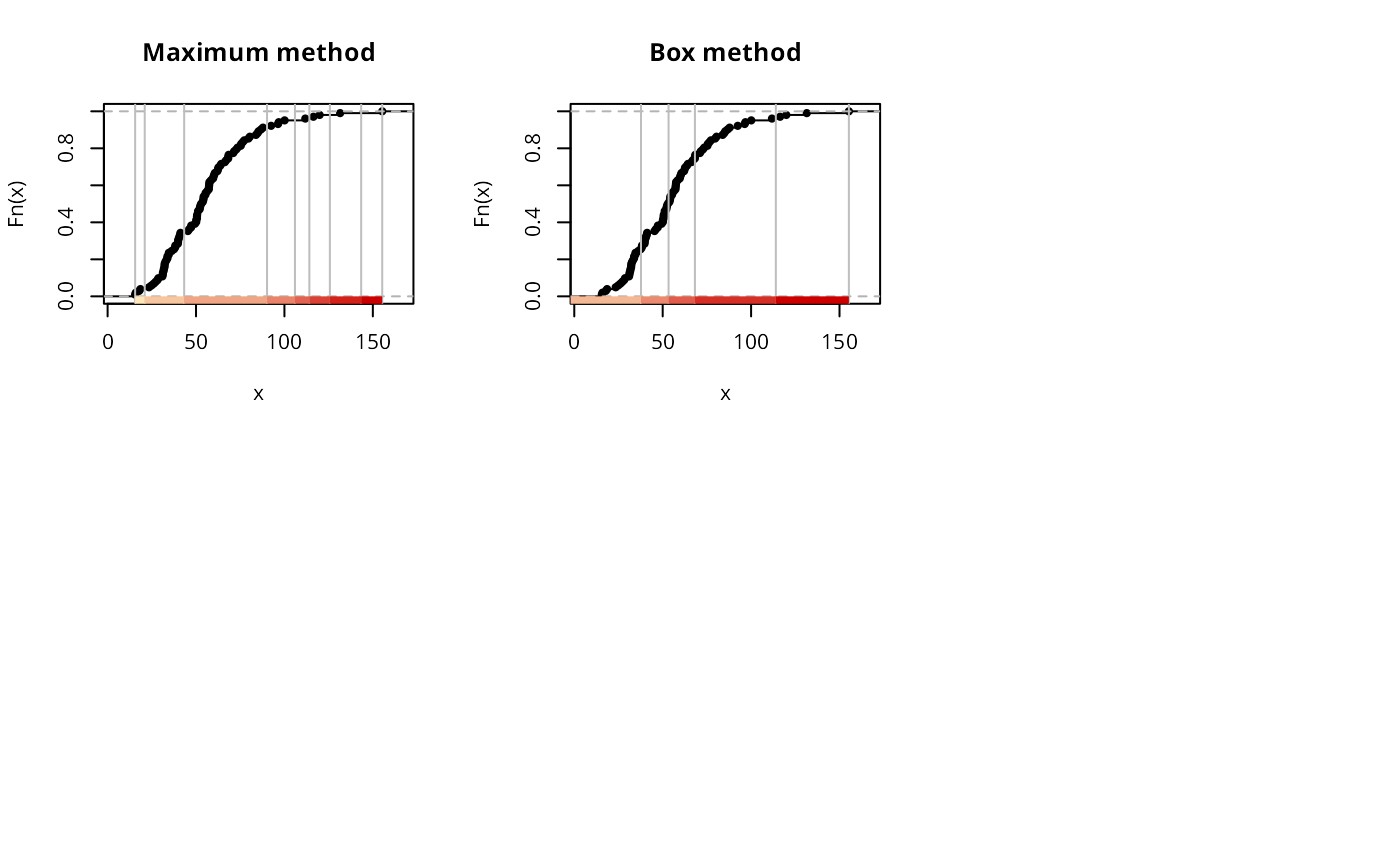
plot(classIntervals(jenks71$jenks71, style="maximum"), pal=pal1,
main="Maximum method")
plot(classIntervals(jenks71$jenks71, style="box"), pal=pal1,
main="Box method")
par(opar)
}
if (run) {
plot(classIntervals(jenks71$jenks71, style="maximum"), pal=pal1,
main="Maximum method")
plot(classIntervals(jenks71$jenks71, style="box"), pal=pal1,
main="Box method")
par(opar)
}
 if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="fixed",
fixedBreaks=c(15.57, 25, 50, 75, 100, 155.30)))
}
#> style: fixed
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,25) [25,50) [50,75) [75,100) [100,155.3]
#> 6 34 42 14 6
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="sd"))
}
#> style: sd
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [5.514407,30.89691) [30.89691,56.27941) [56.27941,81.66191) [81.66191,107.0444)
#> 10 47 31 9
#> [107.0444,132.4269) [132.4269,157.8094]
#> 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="equal"))
}
#> style: equal
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.516) [43.516,71.462) [71.462,99.408) [99.408,127.354)
#> 35 44 17 4
#> [127.354,155.3]
#> 2
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="quantile"))
}
#> style: quantile
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,33.822) [33.822,50.114) [50.114,57.454) [57.454,73.368) [73.368,155.3]
#> 21 20 20 20 21
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans"))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,36.905) [36.905,53.33) [53.33,72.185) [72.185,105.95) [105.95,155.3]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans", intervalClosure="right"))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,36.905] (36.905,53.33] (53.33,72.185] (72.185,105.95] (105.95,155.3]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans", dataPrecision=0))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [16,37) [37,54) [54,73) [73,106) [106,156]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans"), cutlabels=FALSE)
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> under 36.905 36.905 - 53.33 53.33 - 72.185 72.185 - 105.95 over 105.95
#> 25 26 29 17 5
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="hclust", method="complete"))
}
#> style: hclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,54.81) [54.81,74.405) [74.405,105.95) [105.95,143.4) [143.4,155.3]
#> 55 27 15 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="hclust", method="single"))
}
#> style: hclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,20.995) [20.995,105.95) [105.95,125.7) [125.7,143.4) [143.4,155.3]
#> 4 93 3 1 1
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="bclust", verbose=FALSE))
}
#> style: bclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,82.175) [82.175,105.95) [105.95,143.4) [143.4,155.3]
#> 35 53 9 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="bclust",
hclust.method="complete", verbose=FALSE))
}
#> style: bclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,82.175) [82.175,105.95) [105.95,143.4) [143.4,155.3]
#> 35 53 9 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="fisher"))
}
#> style: fisher
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,61.36) [61.36,78.475) [78.475,105.95) [105.95,155.3]
#> 35 33 18 11 5
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="jenks"))
}
#> style: jenks
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,41.2] (41.2,60.66] (60.66,77.29] (77.29,100.1] (100.1,155.3]
#> 35 33 18 11 5
if (run) {
print(classIntervals(jenks71$jenks71, style="dpih"))
}
#> style: dpih
#> one of 16,007,560,800 possible partitions of this variable into 8 classes
#> [15.57,31.70792) [31.70792,47.84584) [47.84584,63.98376) [63.98376,80.12169)
#> 14 25 33 15
#> [80.12169,96.25961) [96.25961,112.3975) [112.3975,128.5355) [128.5355,144.6734]
#> 7 4 2 2
if (run) {
print(classIntervals(jenks71$jenks71, style="dpih", range.x=c(0, 160)))
}
#> style: dpih
#> one of 186,087,894,300 possible partitions of this variable into 9 classes
#> [0,16.26458) [16.26458,32.52917) [32.52917,48.79375) [48.79375,65.05834)
#> 2 16 21 34
#> [65.05834,81.32292) [81.32292,97.58751) [97.58751,113.8521) [113.8521,130.1167)
#> 15 8 2 2
#> [130.1167,146.3813]
#> 2
if (run) {
print(classIntervals(jenks71$jenks71, style="headtails"))
}
#> style: headtails
#> one of 100 possible partitions of this variable into 2 classes
#> [15.57,56.27941) [56.27941,155.3]
#> 57 45
if (run) {
print(classIntervals(jenks71$jenks71, style="headtails", thr = .45))
}
#> style: headtails
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [15.57,56.27941) [56.27941,77.74533) [77.74533,100.5925) [100.5925,126.98)
#> 57 29 11 3
#> [126.98,143.4) [143.4,155.3]
#> 1 1
if (run) {
print(classIntervals(jenks71$jenks71, style="maximum"))
}
#> style: maximum
#> one of 16,007,560,800 possible partitions of this variable into 8 classes
#> [15.57,20.995) [20.995,43.3) [43.3,90.16) [90.16,105.95) [105.95,114.1)
#> 4 31 58 4 1
#> [114.1,125.7) [125.7,143.4) [143.4,155.3]
#> 2 1 1
if (run) {
print(classIntervals(jenks71$jenks71, style="box"))
}
#> style: box
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [-Inf,-8.02125) [-8.02125,37.7325) [37.7325,53.33) [53.33,68.235)
#> 0 26 25 25
#> [68.235,113.9887) [113.9887,155.3]
#> 22 4
if (run) {
print(classIntervals(jenks71$jenks71, style="box", iqr_mult = 0.25))
}
#> style: box
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [15.57,30.10688) [30.10688,37.7325) [37.7325,53.33) [53.33,68.235)
#> 10 16 25 25
#> [68.235,75.86062) [75.86062,155.3]
#> 8 18
x <- c(0, 0, 0, 1, 2, 50)
print(classIntervals(x, n=3, style="fisher"))
#> style: fisher
#> one of 3 possible partitions of this variable into 3 classes
#> [0,0.5) [0.5,26) [26,50]
#> 3 2 1
print(classIntervals(x, n=3, style="jenks"))
#> style: jenks
#> one of 3 possible partitions of this variable into 3 classes
#> [0,0] (0,2] (2,50]
#> 3 2 1
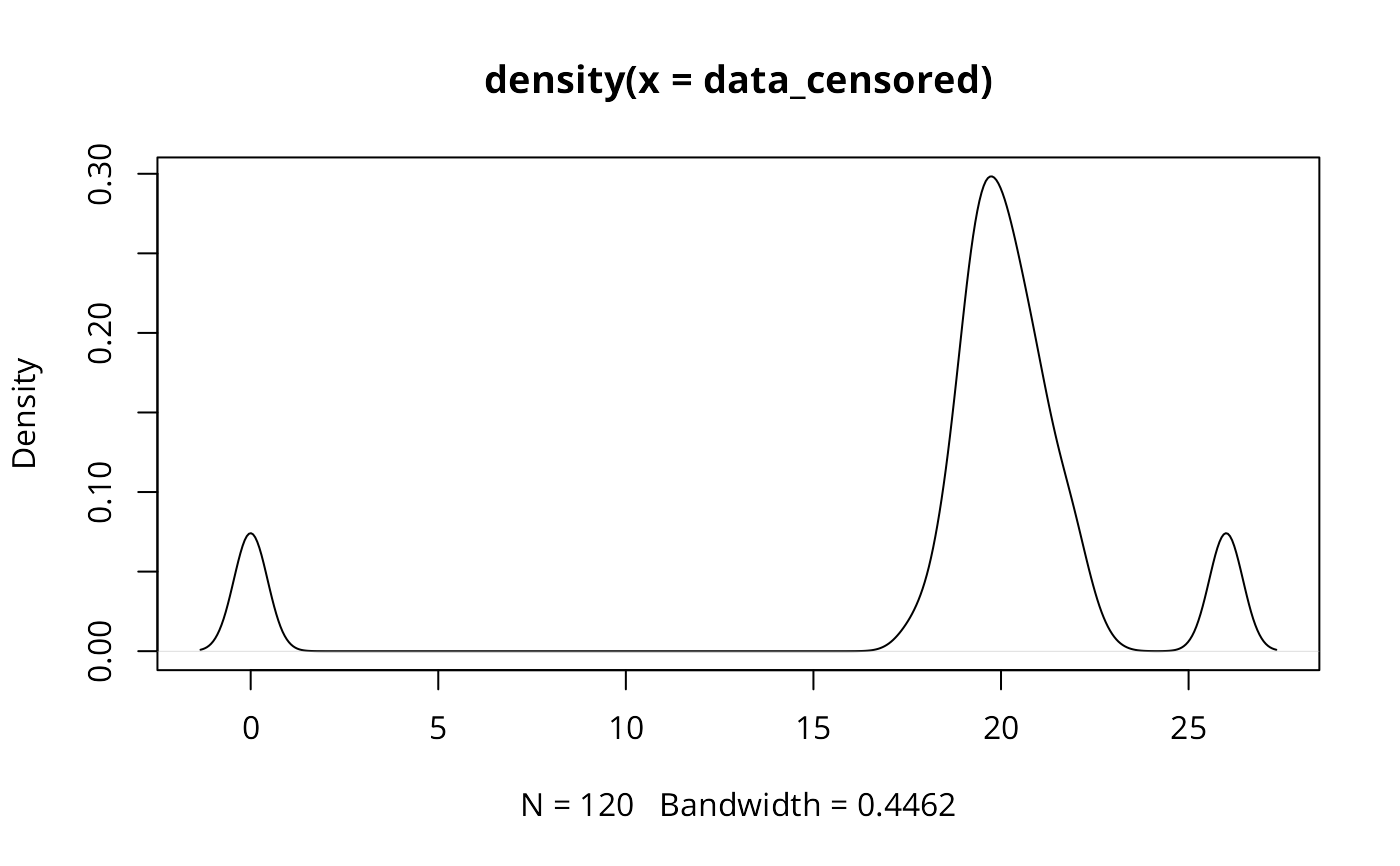
# Argument 'unique' will collapse the label of classes containing a
# single value. This is particularly useful for 'censored' variables
# that contain for example many zeros.
data_censored<-c(rep(0,10), rnorm(100, mean=20,sd=1),rep(26,10))
plot(density(data_censored))
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="fixed",
fixedBreaks=c(15.57, 25, 50, 75, 100, 155.30)))
}
#> style: fixed
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,25) [25,50) [50,75) [75,100) [100,155.3]
#> 6 34 42 14 6
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="sd"))
}
#> style: sd
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [5.514407,30.89691) [30.89691,56.27941) [56.27941,81.66191) [81.66191,107.0444)
#> 10 47 31 9
#> [107.0444,132.4269) [132.4269,157.8094]
#> 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="equal"))
}
#> style: equal
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.516) [43.516,71.462) [71.462,99.408) [99.408,127.354)
#> 35 44 17 4
#> [127.354,155.3]
#> 2
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="quantile"))
}
#> style: quantile
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,33.822) [33.822,50.114) [50.114,57.454) [57.454,73.368) [73.368,155.3]
#> 21 20 20 20 21
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans"))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,36.905) [36.905,53.33) [53.33,72.185) [72.185,105.95) [105.95,155.3]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans", intervalClosure="right"))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,36.905] (36.905,53.33] (53.33,72.185] (72.185,105.95] (105.95,155.3]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans", dataPrecision=0))
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [16,37) [37,54) [54,73) [73,106) [106,156]
#> 25 26 29 17 5
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="kmeans"), cutlabels=FALSE)
}
#> style: kmeans
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> under 36.905 36.905 - 53.33 53.33 - 72.185 72.185 - 105.95 over 105.95
#> 25 26 29 17 5
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="hclust", method="complete"))
}
#> style: hclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,54.81) [54.81,74.405) [74.405,105.95) [105.95,143.4) [143.4,155.3]
#> 55 27 15 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="hclust", method="single"))
}
#> style: hclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,20.995) [20.995,105.95) [105.95,125.7) [125.7,143.4) [143.4,155.3]
#> 4 93 3 1 1
if (run) {
set.seed(1)
print(classIntervals(jenks71$jenks71, n=5, style="bclust", verbose=FALSE))
}
#> style: bclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,82.175) [82.175,105.95) [105.95,143.4) [143.4,155.3]
#> 35 53 9 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="bclust",
hclust.method="complete", verbose=FALSE))
}
#> style: bclust
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,82.175) [82.175,105.95) [105.95,143.4) [143.4,155.3]
#> 35 53 9 4 1
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="fisher"))
}
#> style: fisher
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,43.3) [43.3,61.36) [61.36,78.475) [78.475,105.95) [105.95,155.3]
#> 35 33 18 11 5
if (run) {
print(classIntervals(jenks71$jenks71, n=5, style="jenks"))
}
#> style: jenks
#> one of 3,921,225 possible partitions of this variable into 5 classes
#> [15.57,41.2] (41.2,60.66] (60.66,77.29] (77.29,100.1] (100.1,155.3]
#> 35 33 18 11 5
if (run) {
print(classIntervals(jenks71$jenks71, style="dpih"))
}
#> style: dpih
#> one of 16,007,560,800 possible partitions of this variable into 8 classes
#> [15.57,31.70792) [31.70792,47.84584) [47.84584,63.98376) [63.98376,80.12169)
#> 14 25 33 15
#> [80.12169,96.25961) [96.25961,112.3975) [112.3975,128.5355) [128.5355,144.6734]
#> 7 4 2 2
if (run) {
print(classIntervals(jenks71$jenks71, style="dpih", range.x=c(0, 160)))
}
#> style: dpih
#> one of 186,087,894,300 possible partitions of this variable into 9 classes
#> [0,16.26458) [16.26458,32.52917) [32.52917,48.79375) [48.79375,65.05834)
#> 2 16 21 34
#> [65.05834,81.32292) [81.32292,97.58751) [97.58751,113.8521) [113.8521,130.1167)
#> 15 8 2 2
#> [130.1167,146.3813]
#> 2
if (run) {
print(classIntervals(jenks71$jenks71, style="headtails"))
}
#> style: headtails
#> one of 100 possible partitions of this variable into 2 classes
#> [15.57,56.27941) [56.27941,155.3]
#> 57 45
if (run) {
print(classIntervals(jenks71$jenks71, style="headtails", thr = .45))
}
#> style: headtails
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [15.57,56.27941) [56.27941,77.74533) [77.74533,100.5925) [100.5925,126.98)
#> 57 29 11 3
#> [126.98,143.4) [143.4,155.3]
#> 1 1
if (run) {
print(classIntervals(jenks71$jenks71, style="maximum"))
}
#> style: maximum
#> one of 16,007,560,800 possible partitions of this variable into 8 classes
#> [15.57,20.995) [20.995,43.3) [43.3,90.16) [90.16,105.95) [105.95,114.1)
#> 4 31 58 4 1
#> [114.1,125.7) [125.7,143.4) [143.4,155.3]
#> 2 1 1
if (run) {
print(classIntervals(jenks71$jenks71, style="box"))
}
#> style: box
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [-Inf,-8.02125) [-8.02125,37.7325) [37.7325,53.33) [53.33,68.235)
#> 0 26 25 25
#> [68.235,113.9887) [113.9887,155.3]
#> 22 4
if (run) {
print(classIntervals(jenks71$jenks71, style="box", iqr_mult = 0.25))
}
#> style: box
#> one of 75,287,520 possible partitions of this variable into 6 classes
#> [15.57,30.10688) [30.10688,37.7325) [37.7325,53.33) [53.33,68.235)
#> 10 16 25 25
#> [68.235,75.86062) [75.86062,155.3]
#> 8 18
x <- c(0, 0, 0, 1, 2, 50)
print(classIntervals(x, n=3, style="fisher"))
#> style: fisher
#> one of 3 possible partitions of this variable into 3 classes
#> [0,0.5) [0.5,26) [26,50]
#> 3 2 1
print(classIntervals(x, n=3, style="jenks"))
#> style: jenks
#> one of 3 possible partitions of this variable into 3 classes
#> [0,0] (0,2] (2,50]
#> 3 2 1
# Argument 'unique' will collapse the label of classes containing a
# single value. This is particularly useful for 'censored' variables
# that contain for example many zeros.
data_censored<-c(rep(0,10), rnorm(100, mean=20,sd=1),rep(26,10))
plot(density(data_censored))
 cl2 <- classIntervals(data_censored, n=5, style="jenks", dataPrecision=2)
print(cl2, unique=FALSE)
#> style: jenks
#> one of 4,082,925 possible partitions of this variable into 5 classes
#> [0,0] (0,19.5] (19.5,20.63] (20.63,22.6] (22.6,26]
#> 10 33 39 28 10
print(cl2, unique=TRUE)
#> style: jenks
#> one of 4,082,925 possible partitions of this variable into 5 classes
#> Class found with one single (possibly repeated) value: changed label
#> 0 (0,19.5] (19.5,20.63] (20.63,22.6] 26
#> 10 33 39 28 10
# \dontrun{
set.seed(1)
n <- 1e+05
x <- runif(n)
classIntervals(x, n=5, style="sd")
#> style: sd
#> [-0.07925682,0.06546355) [0.06546355,0.2101839) [0.2101839,0.3549043)
#> 6597 14579 14403
#> [0.3549043,0.4996247) [0.4996247,0.644345) [0.644345,0.7890654)
#> 14395 14446 14439
#> [0.7890654,0.9337858) [0.9337858,1.078506]
#> 14463 6678
classIntervals(x, n=5, style="pretty")
#> style: pretty
#> [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8) [0.8,1]
#> 20142 19936 19888 19993 20041
classIntervals(x, n=5, style="equal")
#> style: equal
#> [3.895489e-06,0.1999925) [0.1999925,0.3999812) [0.3999812,0.5999698)
#> 20141 19935 19888
#> [0.5999698,0.7999584) [0.7999584,0.9999471]
#> 19991 20045
classIntervals(x, n=5, style="quantile")
#> style: quantile
#> [3.895489e-06,0.1984408) [0.1984408,0.3993007) [0.3993007,0.6003913)
#> 20000 20000 20000
#> [0.6003913,0.8003984) [0.8003984,0.9999471]
#> 20000 20000
# the class intervals found vary a little because of sampling
classIntervals(x, n=5, style="kmeans")
#> style: kmeans
#> [3.895489e-06,0.1992885) [0.1992885,0.4002208) [0.4002208,0.600954)
#> 20075 20034 19946
#> [0.600954,0.800892) [0.800892,0.9999471]
#> 20007 19938
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.2084817) [0.2084817,0.4107739) [0.4107739,0.6097159)
#> 21009 20108 19764
#> [0.6097159,0.8037792) [0.8037792,0.9999471]
#> 19470 19649
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.201632) [0.201632,0.4031747) [0.4031747,0.6060818)
#> 20327 20045 20172
#> [0.6060818,0.8071612) [0.8071612,0.9999471]
#> 20159 19297
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.1927805) [0.1927805,0.3880168) [0.3880168,0.5904186)
#> 19443 19489 20059
#> [0.5904186,0.7963362) [0.7963362,0.9999471]
#> 20617 20392
# }
have_units <- FALSE
if (require(units, quietly=TRUE)) have_units <- TRUE
#> udunits database from /usr/share/udunits/udunits2.xml
if (have_units) {
set.seed(1)
x_units <- set_units(sample(seq(1, 100, 0.25), 100), km/h)
# \dontrun{
classIntervals(x_units, n=5, style="sd")
# }
}
#> style: sd
#> one of 14,887,031,544 possible partitions of this [km/h] variable into 8 classes
#> [-6.990949,7.637413) [7.637413,22.26578) [22.26578,36.89414)
#> 6 15 16
#> [36.89414,51.5225) [51.5225,66.15086) [66.15086,80.77922)
#> 12 12 16
#> [80.77922,95.40759) [95.40759,110.0359]
#> 18 5
if (have_units) {
classIntervals(x_units, n=5, style="pretty")
}
#> style: pretty
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [0,20) [20,40) [40,60) [60,80) [80,100]
#> 18 21 19 19 23
if (have_units) {
# \dontrun{
classIntervals(x_units, n=5, style="equal")
# }
}
#> style: equal
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,23.1) [23.1,42.2) [42.2,61.3) [61.3,80.4) [80.4,99.5]
#> 22 19 17 19 23
if (have_units) {
classIntervals(x_units, n=5, style="quantile")
}
#> style: quantile
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,21.95) [21.95,41.5) [41.5,64.05) [64.05,82.8) [82.8,99.5]
#> 20 20 20 20 20
if (have_units) {
# \dontrun{
classIntervals(x_units, n=5, style="kmeans")
# }
}
#> style: kmeans
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,19.375) [19.375,39.375) [39.375,60.5) [60.5,79.625) [79.625,99.5]
#> 18 21 19 19 23
if (have_units) {
classIntervals(x_units, n=5, style="fisher")
}
#> style: fisher
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,19.375) [19.375,39.375) [39.375,60.5) [60.5,79.625) [79.625,99.5]
#> 18 21 19 19 23
if (have_units) {
classIntervals(x_units, style="headtails")
}
#> style: headtails
#> one of 99 possible partitions of this [km/h] variable into 2 classes
#> [4,51.5225) [51.5225,99.5]
#> 49 51
if (have_units) {
classIntervals(x_units, style="box")
}
#> style: box
#> one of 71,523,144 possible partitions of this [km/h] variable into 6 classes
#> [-Inf,-46.375) [-46.375,26.9375) [26.9375,52) [52,75.8125)
#> 0 25 25 25
#> [75.8125,149.125) [149.125,Inf]
#> 25 0
# \dontrun{
st <- Sys.time()
x_POSIXt <- sample(st+((0:500)*3600), 100)
fx <- st+((0:5)*3600)*100
classIntervals(x_POSIXt, style="fixed", fixedBreaks=fx)
#> style: fixed
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 10:41:00.252928,2024-12-31 14:41:00.252928)
#> 21
#> [2024-12-31 14:41:00.252928,2025-01-04 18:41:00.252928)
#> 18
#> [2025-01-04 18:41:00.252928,2025-01-08 22:41:00.252928)
#> 19
#> [2025-01-08 22:41:00.252928,2025-01-13 02:41:00.252928)
#> 21
#> [2025-01-13 02:41:00.252928,2025-01-17 06:41:00.252928]
#> 21
classIntervals(x_POSIXt, n=5, style="sd")
#> style: sd
#> one of 14,887,031,544 possible partitions of this variable into 8 classes
#> [2024-12-25 13:40:28.307138,2024-12-28 14:46:36.293586)
#> 5
#> [2024-12-28 14:46:36.293586,2024-12-31 15:52:44.280033)
#> 16
#> [2024-12-31 15:52:44.280033,2025-01-03 16:58:52.266481)
#> 17
#> [2025-01-03 16:58:52.266481,2025-01-06 18:05:00.252928)
#> 12
#> [2025-01-06 18:05:00.252928,2025-01-09 19:11:08.239376)
#> 14
#> [2025-01-09 19:11:08.239376,2025-01-12 20:17:16.225824)
#> 14
#> [2025-01-12 20:17:16.225824,2025-01-15 21:23:24.212271)
#> 16
#> [2025-01-15 21:23:24.212271,2025-01-18 22:29:32.19871]
#> 6
classIntervals(x_POSIXt, n=5, style="pretty")
#> style: pretty
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-24 01:26:40,2024-12-29 20:20:00)
#> 12
#> [2024-12-29 20:20:00,2025-01-04 15:13:20)
#> 27
#> [2025-01-04 15:13:20,2025-01-10 10:06:40)
#> 28
#> [2025-01-10 10:06:40,2025-01-16 05:00:00)
#> 28
#> [2025-01-16 05:00:00,2025-01-21 23:53:20]
#> 5
classIntervals(x_POSIXt, n=5, style="equal")
#> style: equal
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2025-01-01 00:05:00.252928)
#> 23
#> [2025-01-01 00:05:00.252928,2025-01-05 00:29:00.252928)
#> 16
#> [2025-01-05 00:29:00.252928,2025-01-09 00:53:00.252928)
#> 19
#> [2025-01-09 00:53:00.252928,2025-01-13 01:17:00.252928)
#> 20
#> [2025-01-13 01:17:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, n=5, style="quantile")
#> style: quantile
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 10:29:00.252928)
#> 20
#> [2024-12-31 10:29:00.252928,2025-01-05 03:41:00.252928)
#> 20
#> [2025-01-05 03:41:00.252928,2025-01-09 03:05:00.252928)
#> 20
#> [2025-01-09 03:05:00.252928,2025-01-13 05:17:00.252928)
#> 20
#> [2025-01-13 05:17:00.252928,2025-01-17 01:41:00.252928]
#> 20
classIntervals(x_POSIXt, n=5, style="kmeans")
#> style: kmeans
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 02:41:00.252928)
#> 19
#> [2024-12-31 02:41:00.252928,2025-01-04 01:41:00.252928)
#> 19
#> [2025-01-04 01:41:00.252928,2025-01-08 10:11:00.252928)
#> 17
#> [2025-01-08 10:11:00.252928,2025-01-12 14:11:00.252928)
#> 23
#> [2025-01-12 14:11:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, n=5, style="fisher")
#> style: fisher
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 02:41:00.252928)
#> 19
#> [2024-12-31 02:41:00.252928,2025-01-04 01:41:00.252928)
#> 19
#> [2025-01-04 01:41:00.252928,2025-01-08 10:11:00.252928)
#> 17
#> [2025-01-08 10:11:00.252928,2025-01-12 14:11:00.252928)
#> 23
#> [2025-01-12 14:11:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, style="headtails")
#> style: headtails
#> one of 99 possible partitions of this variable into 2 classes
#> [2024-12-27 23:41:00.252928,2025-01-06 18:05:00.252928)
#> 50
#> [2025-01-06 18:05:00.252928,2025-01-17 01:41:00.252928]
#> 50
classIntervals(x_POSIXt, style="maximum")
#> style: maximum
#> one of 14,887,031,544 possible partitions of this variable into 8 classes
#> [2024-12-27 23:41:00.252928,2025-01-03 08:41:00.252928)
#> 37
#> [2025-01-03 08:41:00.252928,2025-01-04 01:41:00.252928)
#> 1
#> [2025-01-04 01:41:00.252928,2025-01-04 18:11:00.252928)
#> 1
#> [2025-01-04 18:11:00.252928,2025-01-07 02:41:00.252928)
#> 12
#> [2025-01-07 02:41:00.252928,2025-01-10 09:41:00.252928)
#> 16
#> [2025-01-10 09:41:00.252928,2025-01-12 14:11:00.252928)
#> 11
#> [2025-01-12 14:11:00.252928,2025-01-15 22:11:00.252928)
#> 16
#> [2025-01-15 22:11:00.252928,2025-01-17 01:41:00.252928]
#> 6
classIntervals(x_POSIXt, style="box")
#> style: box
#> one of 71,523,144 possible partitions of this variable into 6 classes
#> [-Inf,2024-12-17 03:03:30.252928)
#> 0
#> [2024-12-17 03:03:30.252928,2025-01-01 10:11:00.252928)
#> 25
#> [2025-01-01 10:11:00.252928,2025-01-06 17:41:00.252928)
#> 25
#> [2025-01-06 17:41:00.252928,2025-01-11 14:56:00.252928)
#> 25
#> [2025-01-11 14:56:00.252928,2025-01-26 22:03:30.252928)
#> 25
#> [2025-01-26 22:03:30.252928,Inf]
#> 0
# }
# see vignette for further details
# \dontrun{
# Head Tails method is suitable for right-sided heavy-tailed distributions
set.seed(1234)
# Heavy tails-----
# Pareto distributions a=7 b=14
paretodist <- 7 / (1 - runif(100)) ^ (1 / 14)
# Lognorm
lognormdist <- rlnorm(100)
# Weibull
weibulldist <- rweibull(100, 1, scale = 5)
pal1 <- c("wheat1", "red3")
opar <- par(mfrow = c(1, 3))
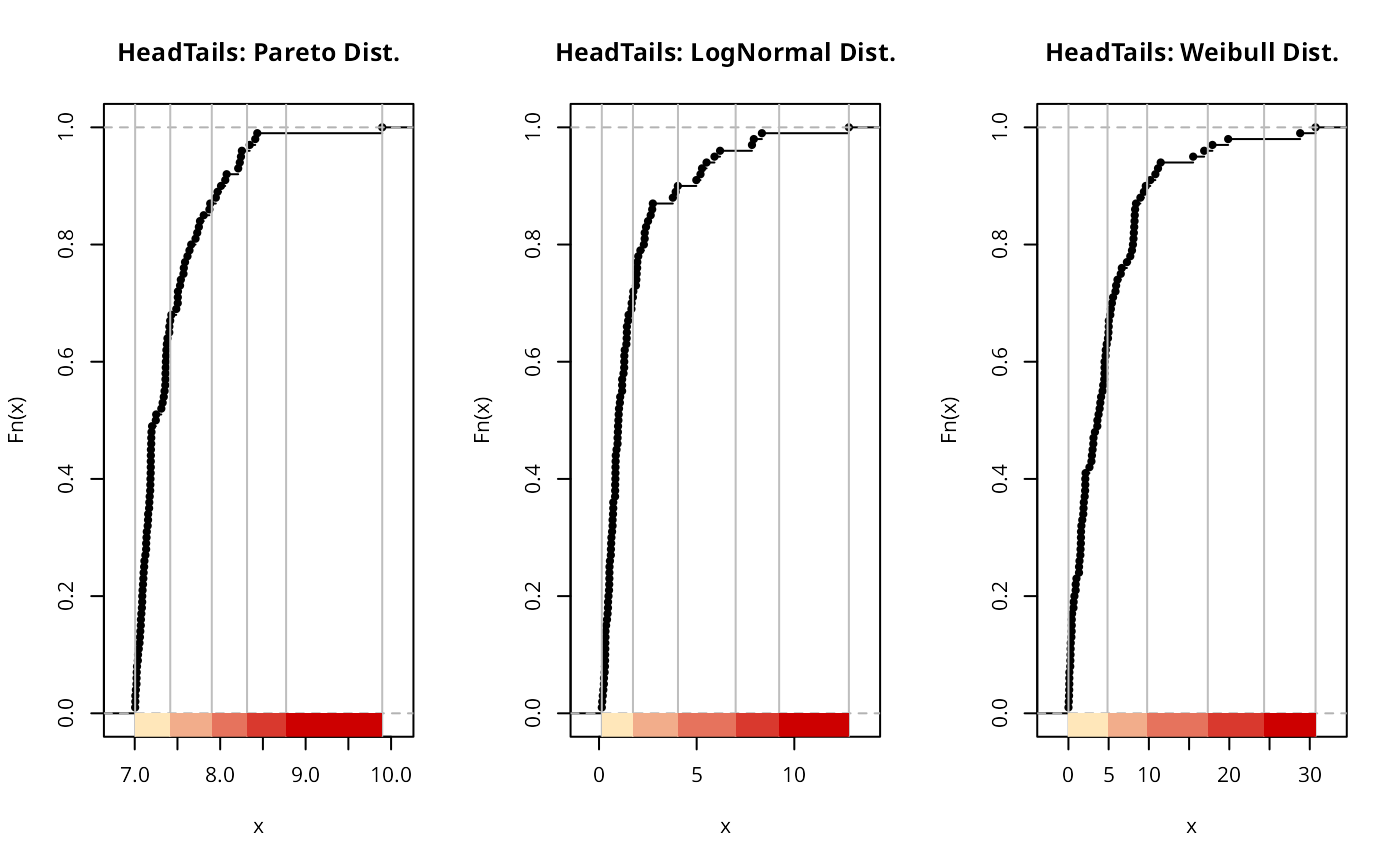
plot(classIntervals(paretodist, style = "headtails"),
pal = pal1,
main = "HeadTails: Pareto Dist.")
plot(classIntervals(lognormdist, style = "headtails"),
pal = pal1,
main = "HeadTails: LogNormal Dist.")
plot(classIntervals(weibulldist, style = "headtails"),
pal = pal1,
main = "HeadTails: Weibull Dist.")
cl2 <- classIntervals(data_censored, n=5, style="jenks", dataPrecision=2)
print(cl2, unique=FALSE)
#> style: jenks
#> one of 4,082,925 possible partitions of this variable into 5 classes
#> [0,0] (0,19.5] (19.5,20.63] (20.63,22.6] (22.6,26]
#> 10 33 39 28 10
print(cl2, unique=TRUE)
#> style: jenks
#> one of 4,082,925 possible partitions of this variable into 5 classes
#> Class found with one single (possibly repeated) value: changed label
#> 0 (0,19.5] (19.5,20.63] (20.63,22.6] 26
#> 10 33 39 28 10
# \dontrun{
set.seed(1)
n <- 1e+05
x <- runif(n)
classIntervals(x, n=5, style="sd")
#> style: sd
#> [-0.07925682,0.06546355) [0.06546355,0.2101839) [0.2101839,0.3549043)
#> 6597 14579 14403
#> [0.3549043,0.4996247) [0.4996247,0.644345) [0.644345,0.7890654)
#> 14395 14446 14439
#> [0.7890654,0.9337858) [0.9337858,1.078506]
#> 14463 6678
classIntervals(x, n=5, style="pretty")
#> style: pretty
#> [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8) [0.8,1]
#> 20142 19936 19888 19993 20041
classIntervals(x, n=5, style="equal")
#> style: equal
#> [3.895489e-06,0.1999925) [0.1999925,0.3999812) [0.3999812,0.5999698)
#> 20141 19935 19888
#> [0.5999698,0.7999584) [0.7999584,0.9999471]
#> 19991 20045
classIntervals(x, n=5, style="quantile")
#> style: quantile
#> [3.895489e-06,0.1984408) [0.1984408,0.3993007) [0.3993007,0.6003913)
#> 20000 20000 20000
#> [0.6003913,0.8003984) [0.8003984,0.9999471]
#> 20000 20000
# the class intervals found vary a little because of sampling
classIntervals(x, n=5, style="kmeans")
#> style: kmeans
#> [3.895489e-06,0.1992885) [0.1992885,0.4002208) [0.4002208,0.600954)
#> 20075 20034 19946
#> [0.600954,0.800892) [0.800892,0.9999471]
#> 20007 19938
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.2084817) [0.2084817,0.4107739) [0.4107739,0.6097159)
#> 21009 20108 19764
#> [0.6097159,0.8037792) [0.8037792,0.9999471]
#> 19470 19649
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.201632) [0.201632,0.4031747) [0.4031747,0.6060818)
#> 20327 20045 20172
#> [0.6060818,0.8071612) [0.8071612,0.9999471]
#> 20159 19297
classIntervals(x, n=5, style="fisher")
#> Warning: N is large, and some styles will run very slowly; sampling imposed
#> style: fisher
#> [3.895489e-06,0.1927805) [0.1927805,0.3880168) [0.3880168,0.5904186)
#> 19443 19489 20059
#> [0.5904186,0.7963362) [0.7963362,0.9999471]
#> 20617 20392
# }
have_units <- FALSE
if (require(units, quietly=TRUE)) have_units <- TRUE
#> udunits database from /usr/share/udunits/udunits2.xml
if (have_units) {
set.seed(1)
x_units <- set_units(sample(seq(1, 100, 0.25), 100), km/h)
# \dontrun{
classIntervals(x_units, n=5, style="sd")
# }
}
#> style: sd
#> one of 14,887,031,544 possible partitions of this [km/h] variable into 8 classes
#> [-6.990949,7.637413) [7.637413,22.26578) [22.26578,36.89414)
#> 6 15 16
#> [36.89414,51.5225) [51.5225,66.15086) [66.15086,80.77922)
#> 12 12 16
#> [80.77922,95.40759) [95.40759,110.0359]
#> 18 5
if (have_units) {
classIntervals(x_units, n=5, style="pretty")
}
#> style: pretty
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [0,20) [20,40) [40,60) [60,80) [80,100]
#> 18 21 19 19 23
if (have_units) {
# \dontrun{
classIntervals(x_units, n=5, style="equal")
# }
}
#> style: equal
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,23.1) [23.1,42.2) [42.2,61.3) [61.3,80.4) [80.4,99.5]
#> 22 19 17 19 23
if (have_units) {
classIntervals(x_units, n=5, style="quantile")
}
#> style: quantile
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,21.95) [21.95,41.5) [41.5,64.05) [64.05,82.8) [82.8,99.5]
#> 20 20 20 20 20
if (have_units) {
# \dontrun{
classIntervals(x_units, n=5, style="kmeans")
# }
}
#> style: kmeans
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,19.375) [19.375,39.375) [39.375,60.5) [60.5,79.625) [79.625,99.5]
#> 18 21 19 19 23
if (have_units) {
classIntervals(x_units, n=5, style="fisher")
}
#> style: fisher
#> one of 3,764,376 possible partitions of this [km/h] variable into 5 classes
#> [4,19.375) [19.375,39.375) [39.375,60.5) [60.5,79.625) [79.625,99.5]
#> 18 21 19 19 23
if (have_units) {
classIntervals(x_units, style="headtails")
}
#> style: headtails
#> one of 99 possible partitions of this [km/h] variable into 2 classes
#> [4,51.5225) [51.5225,99.5]
#> 49 51
if (have_units) {
classIntervals(x_units, style="box")
}
#> style: box
#> one of 71,523,144 possible partitions of this [km/h] variable into 6 classes
#> [-Inf,-46.375) [-46.375,26.9375) [26.9375,52) [52,75.8125)
#> 0 25 25 25
#> [75.8125,149.125) [149.125,Inf]
#> 25 0
# \dontrun{
st <- Sys.time()
x_POSIXt <- sample(st+((0:500)*3600), 100)
fx <- st+((0:5)*3600)*100
classIntervals(x_POSIXt, style="fixed", fixedBreaks=fx)
#> style: fixed
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 10:41:00.252928,2024-12-31 14:41:00.252928)
#> 21
#> [2024-12-31 14:41:00.252928,2025-01-04 18:41:00.252928)
#> 18
#> [2025-01-04 18:41:00.252928,2025-01-08 22:41:00.252928)
#> 19
#> [2025-01-08 22:41:00.252928,2025-01-13 02:41:00.252928)
#> 21
#> [2025-01-13 02:41:00.252928,2025-01-17 06:41:00.252928]
#> 21
classIntervals(x_POSIXt, n=5, style="sd")
#> style: sd
#> one of 14,887,031,544 possible partitions of this variable into 8 classes
#> [2024-12-25 13:40:28.307138,2024-12-28 14:46:36.293586)
#> 5
#> [2024-12-28 14:46:36.293586,2024-12-31 15:52:44.280033)
#> 16
#> [2024-12-31 15:52:44.280033,2025-01-03 16:58:52.266481)
#> 17
#> [2025-01-03 16:58:52.266481,2025-01-06 18:05:00.252928)
#> 12
#> [2025-01-06 18:05:00.252928,2025-01-09 19:11:08.239376)
#> 14
#> [2025-01-09 19:11:08.239376,2025-01-12 20:17:16.225824)
#> 14
#> [2025-01-12 20:17:16.225824,2025-01-15 21:23:24.212271)
#> 16
#> [2025-01-15 21:23:24.212271,2025-01-18 22:29:32.19871]
#> 6
classIntervals(x_POSIXt, n=5, style="pretty")
#> style: pretty
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-24 01:26:40,2024-12-29 20:20:00)
#> 12
#> [2024-12-29 20:20:00,2025-01-04 15:13:20)
#> 27
#> [2025-01-04 15:13:20,2025-01-10 10:06:40)
#> 28
#> [2025-01-10 10:06:40,2025-01-16 05:00:00)
#> 28
#> [2025-01-16 05:00:00,2025-01-21 23:53:20]
#> 5
classIntervals(x_POSIXt, n=5, style="equal")
#> style: equal
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2025-01-01 00:05:00.252928)
#> 23
#> [2025-01-01 00:05:00.252928,2025-01-05 00:29:00.252928)
#> 16
#> [2025-01-05 00:29:00.252928,2025-01-09 00:53:00.252928)
#> 19
#> [2025-01-09 00:53:00.252928,2025-01-13 01:17:00.252928)
#> 20
#> [2025-01-13 01:17:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, n=5, style="quantile")
#> style: quantile
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 10:29:00.252928)
#> 20
#> [2024-12-31 10:29:00.252928,2025-01-05 03:41:00.252928)
#> 20
#> [2025-01-05 03:41:00.252928,2025-01-09 03:05:00.252928)
#> 20
#> [2025-01-09 03:05:00.252928,2025-01-13 05:17:00.252928)
#> 20
#> [2025-01-13 05:17:00.252928,2025-01-17 01:41:00.252928]
#> 20
classIntervals(x_POSIXt, n=5, style="kmeans")
#> style: kmeans
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 02:41:00.252928)
#> 19
#> [2024-12-31 02:41:00.252928,2025-01-04 01:41:00.252928)
#> 19
#> [2025-01-04 01:41:00.252928,2025-01-08 10:11:00.252928)
#> 17
#> [2025-01-08 10:11:00.252928,2025-01-12 14:11:00.252928)
#> 23
#> [2025-01-12 14:11:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, n=5, style="fisher")
#> style: fisher
#> one of 3,764,376 possible partitions of this variable into 5 classes
#> [2024-12-27 23:41:00.252928,2024-12-31 02:41:00.252928)
#> 19
#> [2024-12-31 02:41:00.252928,2025-01-04 01:41:00.252928)
#> 19
#> [2025-01-04 01:41:00.252928,2025-01-08 10:11:00.252928)
#> 17
#> [2025-01-08 10:11:00.252928,2025-01-12 14:11:00.252928)
#> 23
#> [2025-01-12 14:11:00.252928,2025-01-17 01:41:00.252928]
#> 22
classIntervals(x_POSIXt, style="headtails")
#> style: headtails
#> one of 99 possible partitions of this variable into 2 classes
#> [2024-12-27 23:41:00.252928,2025-01-06 18:05:00.252928)
#> 50
#> [2025-01-06 18:05:00.252928,2025-01-17 01:41:00.252928]
#> 50
classIntervals(x_POSIXt, style="maximum")
#> style: maximum
#> one of 14,887,031,544 possible partitions of this variable into 8 classes
#> [2024-12-27 23:41:00.252928,2025-01-03 08:41:00.252928)
#> 37
#> [2025-01-03 08:41:00.252928,2025-01-04 01:41:00.252928)
#> 1
#> [2025-01-04 01:41:00.252928,2025-01-04 18:11:00.252928)
#> 1
#> [2025-01-04 18:11:00.252928,2025-01-07 02:41:00.252928)
#> 12
#> [2025-01-07 02:41:00.252928,2025-01-10 09:41:00.252928)
#> 16
#> [2025-01-10 09:41:00.252928,2025-01-12 14:11:00.252928)
#> 11
#> [2025-01-12 14:11:00.252928,2025-01-15 22:11:00.252928)
#> 16
#> [2025-01-15 22:11:00.252928,2025-01-17 01:41:00.252928]
#> 6
classIntervals(x_POSIXt, style="box")
#> style: box
#> one of 71,523,144 possible partitions of this variable into 6 classes
#> [-Inf,2024-12-17 03:03:30.252928)
#> 0
#> [2024-12-17 03:03:30.252928,2025-01-01 10:11:00.252928)
#> 25
#> [2025-01-01 10:11:00.252928,2025-01-06 17:41:00.252928)
#> 25
#> [2025-01-06 17:41:00.252928,2025-01-11 14:56:00.252928)
#> 25
#> [2025-01-11 14:56:00.252928,2025-01-26 22:03:30.252928)
#> 25
#> [2025-01-26 22:03:30.252928,Inf]
#> 0
# }
# see vignette for further details
# \dontrun{
# Head Tails method is suitable for right-sided heavy-tailed distributions
set.seed(1234)
# Heavy tails-----
# Pareto distributions a=7 b=14
paretodist <- 7 / (1 - runif(100)) ^ (1 / 14)
# Lognorm
lognormdist <- rlnorm(100)
# Weibull
weibulldist <- rweibull(100, 1, scale = 5)
pal1 <- c("wheat1", "red3")
opar <- par(mfrow = c(1, 3))
plot(classIntervals(paretodist, style = "headtails"),
pal = pal1,
main = "HeadTails: Pareto Dist.")
plot(classIntervals(lognormdist, style = "headtails"),
pal = pal1,
main = "HeadTails: LogNormal Dist.")
plot(classIntervals(weibulldist, style = "headtails"),
pal = pal1,
main = "HeadTails: Weibull Dist.")
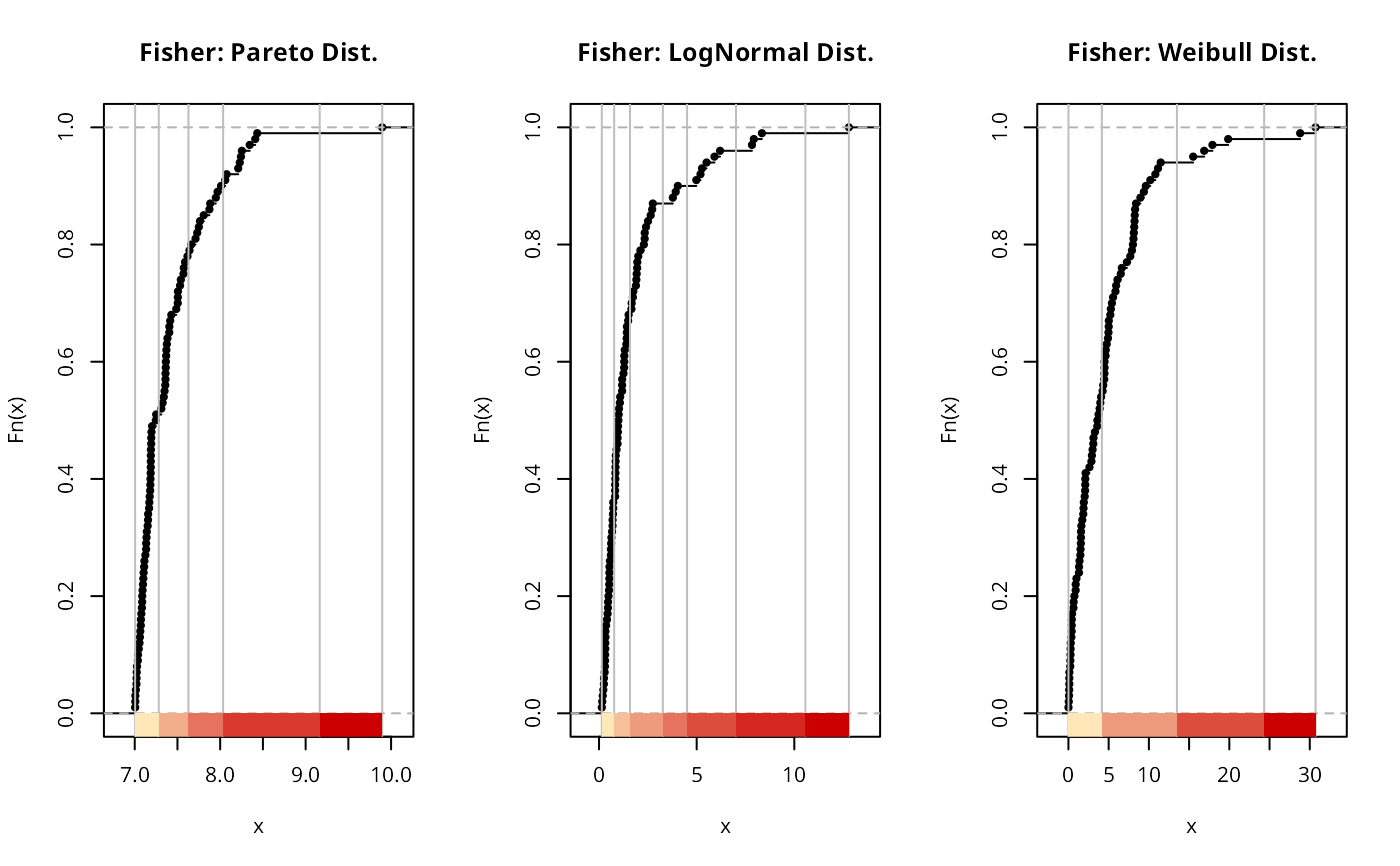
 plot(classIntervals(paretodist, n = 5, style = "fisher"),
pal = pal1,
main = "Fisher: Pareto Dist.")
plot(classIntervals(lognormdist, n = 7, style = "fisher"),
pal = pal1,
main = "Fisher: LogNormal Dist.")
plot(classIntervals(weibulldist, n= 4, style = "fisher"),
pal = pal1,
main = "Fisher: Weibull Dist.")
plot(classIntervals(paretodist, n = 5, style = "fisher"),
pal = pal1,
main = "Fisher: Pareto Dist.")
plot(classIntervals(lognormdist, n = 7, style = "fisher"),
pal = pal1,
main = "Fisher: LogNormal Dist.")
plot(classIntervals(weibulldist, n= 4, style = "fisher"),
pal = pal1,
main = "Fisher: Weibull Dist.")
 par(opar)
#Non heavy tails, thr should be increased-----
#Normal dist
normdist <- rnorm(100)
#Left-tailed truncated Normal distr
leftnorm <- rep(normdist[normdist < mean(normdist)], 2)
# Uniform distribution
unifdist <- runif(100)
opar <- par(mfrow = c(2, 3))
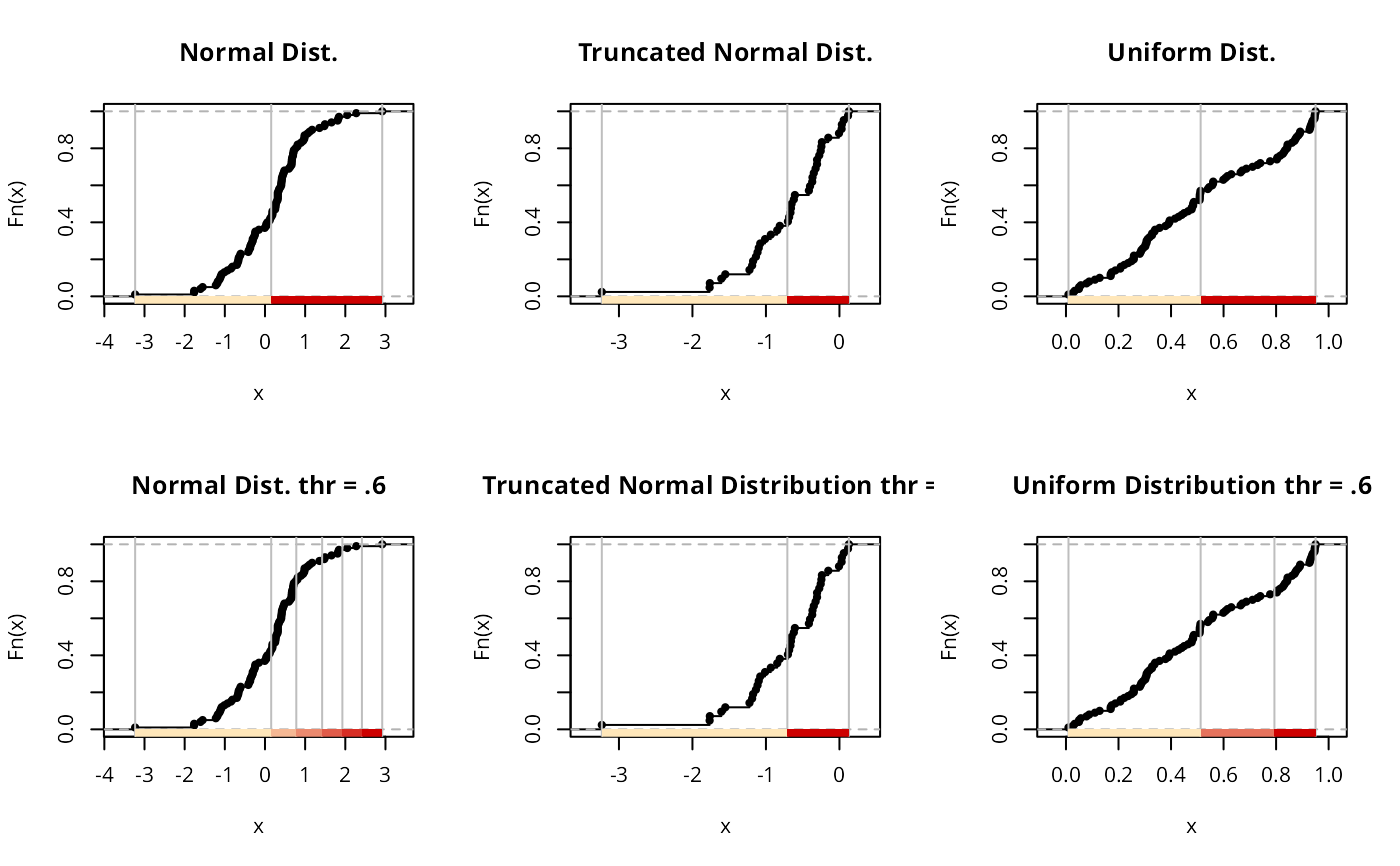
plot(classIntervals(normdist, style = "headtails"),
pal = pal1,
main = "Normal Dist.")
plot(classIntervals(leftnorm, style = "headtails"),
pal = pal1,
main = "Truncated Normal Dist.")
plot(classIntervals(unifdist, style = "headtails"),
pal = pal1,
main = "Uniform Dist.")
# thr should be increased for non heavy-tailed distributions
plot(
classIntervals(normdist, style = "headtails", thr = .6),
pal = pal1,
main = "Normal Dist. thr = .6"
)
plot(
classIntervals(leftnorm, style = "headtails", thr = .6),
pal = pal1,
main = "Truncated Normal Distribution thr = .6"
)
plot(
classIntervals(unifdist, style = "headtails", thr = .6),
pal = pal1,
main = "Uniform Distribution thr = .6"
)
par(opar)
#Non heavy tails, thr should be increased-----
#Normal dist
normdist <- rnorm(100)
#Left-tailed truncated Normal distr
leftnorm <- rep(normdist[normdist < mean(normdist)], 2)
# Uniform distribution
unifdist <- runif(100)
opar <- par(mfrow = c(2, 3))
plot(classIntervals(normdist, style = "headtails"),
pal = pal1,
main = "Normal Dist.")
plot(classIntervals(leftnorm, style = "headtails"),
pal = pal1,
main = "Truncated Normal Dist.")
plot(classIntervals(unifdist, style = "headtails"),
pal = pal1,
main = "Uniform Dist.")
# thr should be increased for non heavy-tailed distributions
plot(
classIntervals(normdist, style = "headtails", thr = .6),
pal = pal1,
main = "Normal Dist. thr = .6"
)
plot(
classIntervals(leftnorm, style = "headtails", thr = .6),
pal = pal1,
main = "Truncated Normal Distribution thr = .6"
)
plot(
classIntervals(unifdist, style = "headtails", thr = .6),
pal = pal1,
main = "Uniform Distribution thr = .6"
)
 par(opar)
# }
par(opar)
# }