Global Empirical Bayes estimator

The function computes global empirical Bayes estimates for rates "shrunk" to the overall mean.

Usage

EBest(n, x, family="poisson")

Arguments

n: a numeric vector of counts of cases
x: a numeric vector of populations at risk
family: either "poisson" for rare conditions or "binomial" for non-rare conditions

Details

Details of the implementation for the "poisson" family are to be found in Marshall, p. 284–5, and Bailey and Gatrell p. 303–306 and exercise 8.2, pp. 328–330. For the "binomial" family, see Martuzzi and Elliott (implementation by Olaf Berke).

Value

A data frame with two columns:

raw: a numerical vector of raw (crude) rates
estmm: a numerical vector of empirical Bayes estimates

and a parameters attribute list with components:

a: global method of moments phi value
m: global method of moments gamma value

References

Marshall R M (1991) Mapping disease and mortality rates using Empirical Bayes Estimators, Applied Statistics, 40, 283–294; Bailey T, Gatrell A (1995) Interactive Spatial Data Analysis, Harlow: Longman, pp. 303–306, Martuzzi M, Elliott P (1996) Empirical Bayes estimation of small area prevalence of non-rare conditions, Statistics in Medicine 15, 1867–1873.

Author

Roger Bivand Roger.Bivand@nhh.no and Olaf Berke, Population Medicine, OVC, University of Guelph, CANADA

Examples

auckland <- st_read(system.file("shapes/auckland.gpkg", package="spData")[1], quiet=TRUE)
res <- EBest(auckland$M77_85, 9*auckland$Und5_81)
attr(res, "parameters")
#> $a
#> [1] 7.284173e-07
#> 
#> $b
#> [1] 0.002633436
#> 
auckland$estmm000 <- res$estmm*1000
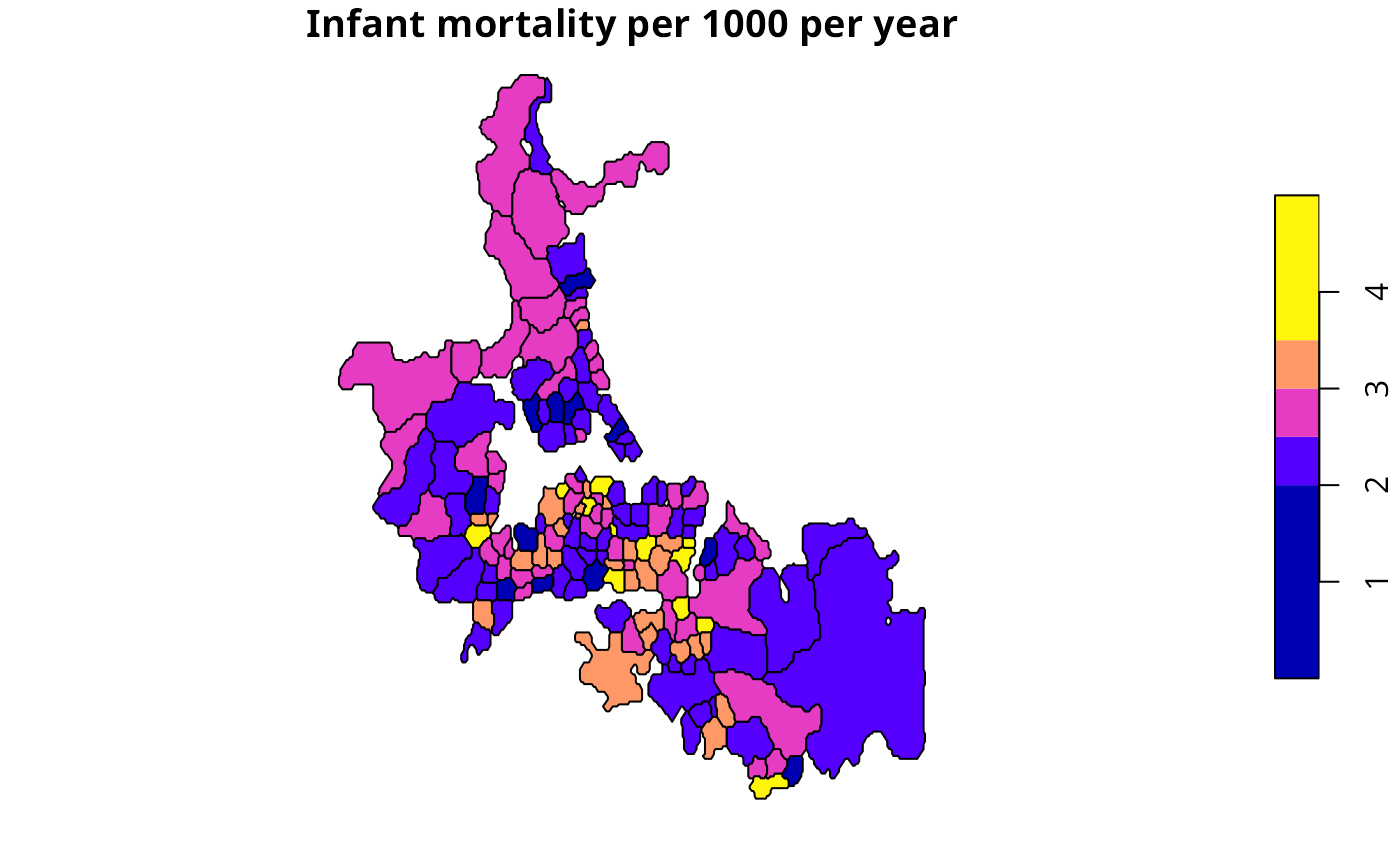
plot(auckland[,"estmm000"], breaks=c(0,2,2.5,3,3.5,5),
 main="Infant mortality per 1000 per year")

data(huddersfield, package="spData")
res <- EBest(huddersfield$cases, huddersfield$total, family="binomial")
round(res[,1:2],4)*100
#>      raw estmm
#> 1  42.86 34.44
#> 2  28.95 29.56
#> 3  28.31 28.94
#> 4  21.43 28.93
#> 5  33.33 30.72
#> 6  30.86 30.43
#> 7  33.70 31.85
#> 8  45.61 35.93
#> 9  26.67 28.95
#> 10 29.41 29.95
#> 11 27.76 28.36
#> 12 33.75 31.75
#> 13 32.67 31.84
#> 14 22.91 25.36
#> 15 34.21 32.33
#> 16 33.77 31.72
#> 17 29.09 29.69
#> 18 15.87 24.36
#> 19 40.91 32.11
#> 20 40.00 31.01
#> 21 28.79 29.53
#> 22 38.89 31.47
#> 23 28.32 29.10
#> 24 33.33 31.44
#> 25 13.95 22.36
#> 26 33.77 31.72
#> 27 31.58 30.31
#> 28 33.33 30.42
#> 29 26.67 28.26
#> 30 63.64 33.57
#> 31 34.38 32.24
#> 32 20.00 27.62
#> 33 19.15 24.60
#> 34 25.53 28.54
#> 35 24.14 27.79
#> 36 44.00 32.98
#> 37 25.33 27.95
#> 38 18.18 26.96
#> 39 31.78 30.97
#> 40 32.20 30.88
#> 41 26.19 28.23
#> 42 19.05 26.65
#> 43 16.67 26.81
#> 44 20.00 28.66
#> 45 32.99 31.54
#> 46 50.00 31.97
#> 47 37.21 32.30
#> 48 32.79 31.13
#> 49 38.89 31.47
#> 50 25.00 27.26
#> 51 26.03 28.29
#> 52 30.43 30.18
#> 53 19.75 25.28
#> 54 50.00 31.61
#> 55 21.62 27.67
#> 56 22.22 27.88
#> 57 36.36 30.71
#> 58 31.25 30.22
#> 59  0.00 29.73
#> 60 29.41 29.95
#> 61 31.16 30.71
#> 62 33.33 30.58
#> 63 33.87 32.22
#> 64 30.00 30.04
#> 65 30.34 30.19
#> 66 40.74 35.00
#> 67 46.43 38.96
#> 68 34.21 31.91
#> 69 24.26 26.10
#> 70 29.41 29.75
#> 71 47.17 39.13