Distance-weighted autocovariate

Calculates the autocovariate to be used in autonormal, autopoisson or autologistic regression. Three distance-weighting schemes are available.

Usage

autocov_dist(z, xy, nbs = 1, type = "inverse", zero.policy = NULL,
 style = "B", longlat=NULL)

Arguments

z: the response variable
xy: a matrix of coordinates or a SpatialPoints, sf or sfc points object
nbs: neighbourhood radius; default is 1
type: the weighting scheme: "one" gives equal weight to all data points in the neighbourhood; "inverse" (the default) weights by inverse distance; "inverse.squared" weights by the square of "inverse"
zero.policy: default NULL, use global option value; if FALSE stop with error for any empty neighbour sets, if TRUE permit the weights list to be formed with zero-length weights vectors
style: default “B” (changed from “W” 2015-01-27); style can take values “W”, “B”, “C”, “U”, and “S”
longlat: TRUE if point coordinates are longitude-latitude decimal, in which case distances are measured in kilometers; if xy is a SpatialPoints object, the value is taken from the object itself

Value

A numeric vector of autocovariate values

Note

The validity of this approach strongly hinges on the correct choice of the neighbourhood scheme! Using style="B" ensures symmetry of the neighbourhood matrix (i.e. \(w_{nm} = w_{mn}\)). Please see Bardos et al. (2015) for details.

References

Augustin N.H., Mugglestone M.A. and Buckland S.T. (1996) An autologistic model for the spatial distribution of wildlife. Journal of Applied Ecology, 33, 339-347; Gumpertz M.L., Graham J.M. and Ristaino J.B. (1997) Autologistic model of spatial pattern of Phytophthora epidemic in bell pepper: effects of soil variables on disease presence. Journal of Agricultural, Biological and Environmental Statistics, 2, 131-156; Bardos, D.C., Guillera-Arroita, G. and Wintle, B.A. (2015) Valid auto-models for spatially autocorrelated occupancy and abundance data. arXiv, 1501.06529.

Author

Carsten F. Dormann and Roger Bivand

Examples

columbus <- st_read(system.file("shapes/columbus.gpkg", package="spData")[1], quiet=TRUE)
#xy <- cbind(columbus$X, columbus$Y)
xy <- st_coordinates(st_centroid(st_geometry(columbus),
 of_largest_polygon=TRUE))
ac1a <- autocov_dist(columbus$CRIME, xy, nbs=10, style="B",
 type="one")
acinva <- autocov_dist(columbus$CRIME, xy, nbs=10, style="B",
 type="inverse")
acinv2a <- autocov_dist(columbus$CRIME, xy, nbs=10, style="B",
 type="inverse.squared")
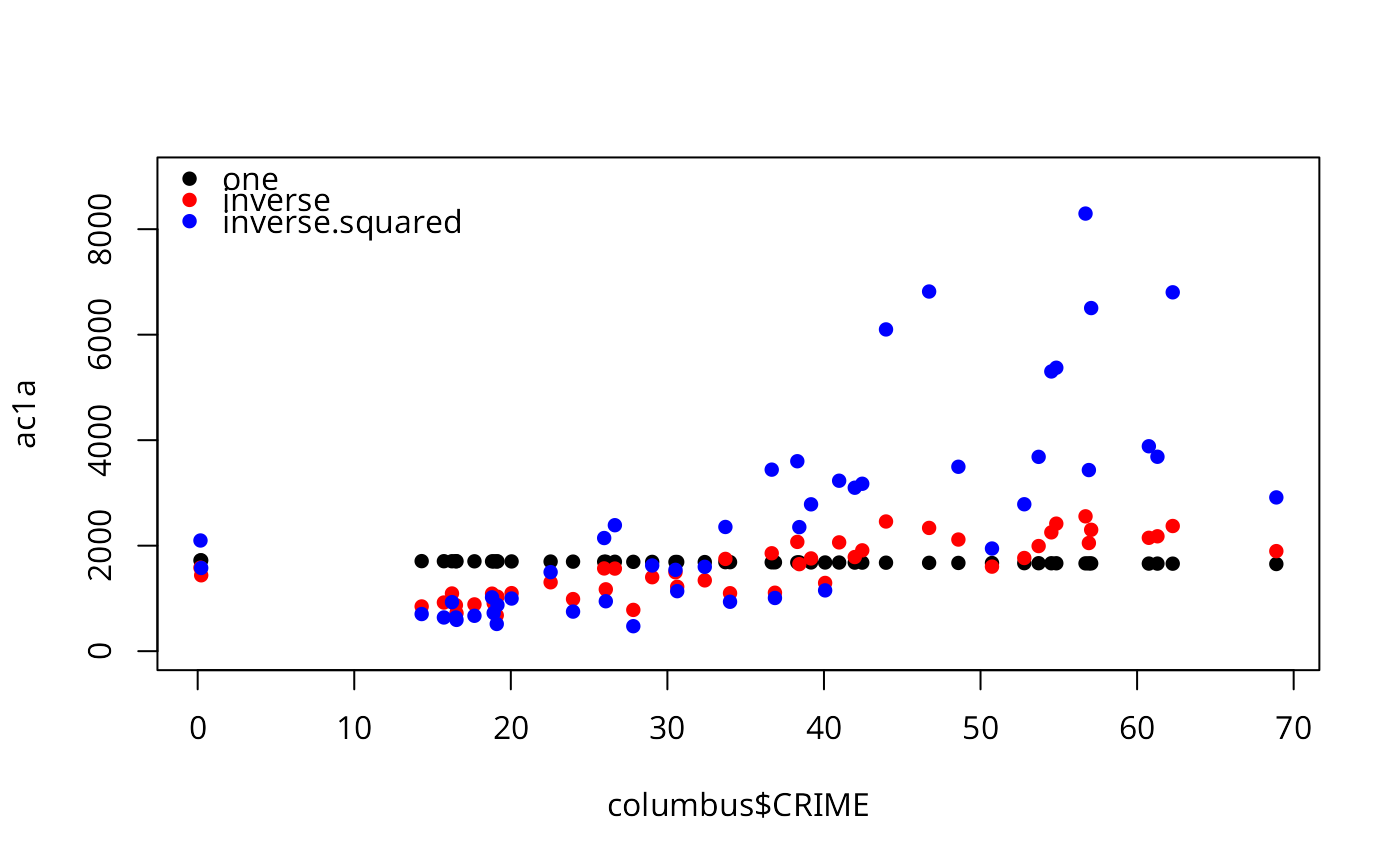
plot(ac1a ~ columbus$CRIME, pch=16, ylim=c(0,9000))
points(acinva ~ columbus$CRIME, pch=16, col="red")
points(acinv2a ~ columbus$CRIME, pch=16, col="blue")
legend("topleft", legend=c("one", "inverse", "inverse.squared"),
 col=c("black", "red", "blue"), bty="n", pch=16)

nb <- dnearneigh(xy, 0, 10)
lw <- nb2listw(nb, style="B")
ac1b <- lag(lw, columbus$CRIME)
all.equal(ac1b, ac1a)
#> [1] TRUE
nbd <- nbdists(nb, xy)
gl <- lapply(nbd, function(x) 1/x)
lw <- nb2listw(nb, glist=gl, style="B")
acinvb <- lag(lw, columbus$CRIME)
all.equal(acinvb, acinva)
#> [1] TRUE
gl2 <- lapply(nbd, function(x) 1/(x^2))
lw <- nb2listw(nb, glist=gl2, style="B")
acinv2b <- lag(lw, columbus$CRIME)
all.equal(acinv2b, acinv2a)
#> [1] TRUE
#xy <- SpatialPoints(xy)
#acinva <- autocov_dist(columbus$CRIME, xy, nbs=10, style="W",
# type="inverse")
#nb <- dnearneigh(xy, 0, 10)
#nbd <- nbdists(nb, xy)
#gl <- lapply(nbd, function(x) 1/x)
#lw <- nb2listw(nb, glist=gl)
#acinvb <- lag(lw, columbus$CRIME)
#all.equal(acinvb, acinva)
acinvc <- autocov_dist(columbus$CRIME, st_centroid(st_geometry(columbus),
 of_largest_polygon=TRUE), nbs=10, style="W", type="inverse")
all.equal(acinvc, acinva)
#> [1] "Mean relative difference: 40.63575"