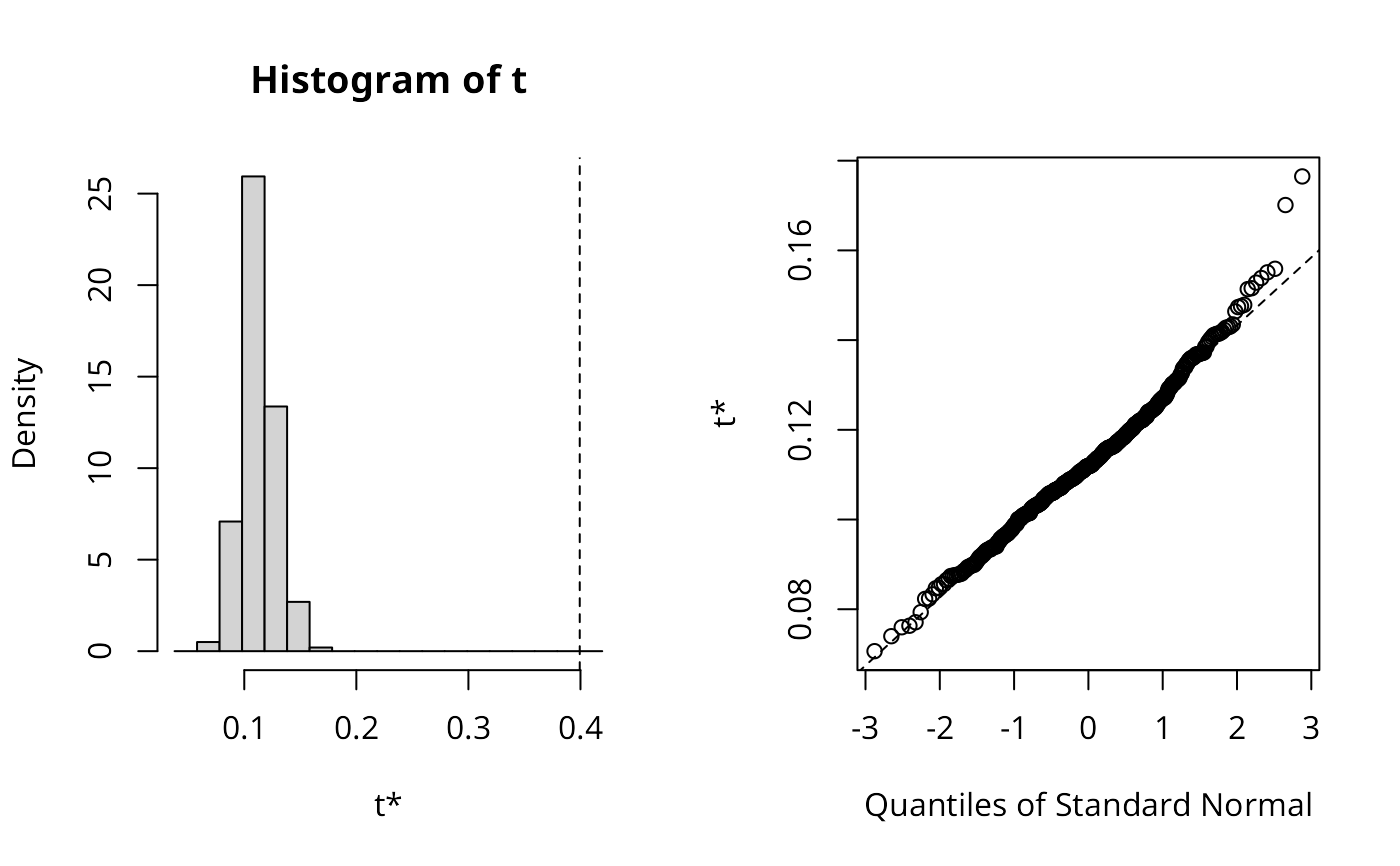Compute the Global Bivariate Moran's I

Given two continuous numeric variables, calculate the bivariate Moran's I. See details for more.

moran_bv(x, y, listw, nsim = 499, scale = TRUE)

Arguments

x

a numeric vector of same length as y.

y

a numeric vector of same length as x.

listw

a listw object for example as created by nb2listw().

nsim

the number of simulations to run.

scale

default TRUE.

Value

An object of class "boot", with the observed statistic in component t0.

Details

The Global Bivariate Moran is defined as

\( I_B = \frac{\Sigma_i(\Sigma_j{w_{ij}y_j\times x_i})}{\Sigma_i{x_i^2}} \)

It is important to note that this is a measure of autocorrelation of X with the spatial lag of Y. As such, the resultant measure may overestimate the amount of spatial autocorrelation which may be a product of the inherent correlation of X and Y. The output object is of class "boot", so that plots and confidence intervals are available using appropriate methods.

References

Wartenberg, D. (1985), Multivariate Spatial Correlation: A Method for Exploratory Geographical Analysis. Geographical Analysis, 17: 263-283. doi:10.1111/j.1538-4632.1985.tb00849.x

Author

Josiah Parry josiah.parry@gmail.com

Examples

data(boston, package = "spData")
x <- boston.c$CRIM
y <- boston.c$NOX
listw <- nb2listw(boston.soi)
set.seed(1)
res_xy <- moran_bv(x, y, listw, nsim=499)
res_xy$t0
#> [1] 0.4082073
boot::boot.ci(res_xy, conf=c(0.99, 0.95, 0.9), type="basic")
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 499 bootstrap replicates
#> 
#> CALL : 
#> boot::boot.ci(boot.out = res_xy, conf = c(0.99, 0.95, 0.9), type = "basic")
#> 
#> Intervals : 
#> Level      Basic         
#> 99%   ( 0.7443,  0.8789 )   
#> 95%   ( 0.7639,  0.8673 )   
#> 90%   ( 0.7739,  0.8615 )  
#> Calculations and Intervals on Original Scale
#> Some basic intervals may be unstable
plot(res_xy)

set.seed(1)
lee_xy <- lee.mc(x, y, listw, nsim=499, return_boot=TRUE)
lee_xy$t0
#> [1] 0.3993476
boot::boot.ci(lee_xy, conf=c(0.99, 0.95, 0.9), type="basic")
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 499 bootstrap replicates
#> 
#> CALL : 
#> boot::boot.ci(boot.out = lee_xy, conf = c(0.99, 0.95, 0.9), type = "basic")
#> 
#> Intervals : 
#> Level      Basic         
#> 99%   ( 0.6363,  0.7236 )   
#> 95%   ( 0.6538,  0.7131 )   
#> 90%   ( 0.6584,  0.7098 )  
#> Calculations and Intervals on Original Scale
#> Some basic intervals may be unstable
plot(lee_xy)

set.seed(1)
res_yx <- moran_bv(y, x, listw, nsim=499)
res_yx$t0
#> [1] 0.4029821
boot::boot.ci(res_yx, conf=c(0.99, 0.95, 0.9), type="basic")
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 499 bootstrap replicates
#> 
#> CALL : 
#> boot::boot.ci(boot.out = res_yx, conf = c(0.99, 0.95, 0.9), type = "basic")
#> 
#> Intervals : 
#> Level      Basic         
#> 99%   ( 0.7301,  0.8729 )   
#> 95%   ( 0.7574,  0.8584 )   
#> 90%   ( 0.7664,  0.8541 )  
#> Calculations and Intervals on Original Scale
#> Some basic intervals may be unstable
plot(res_yx)

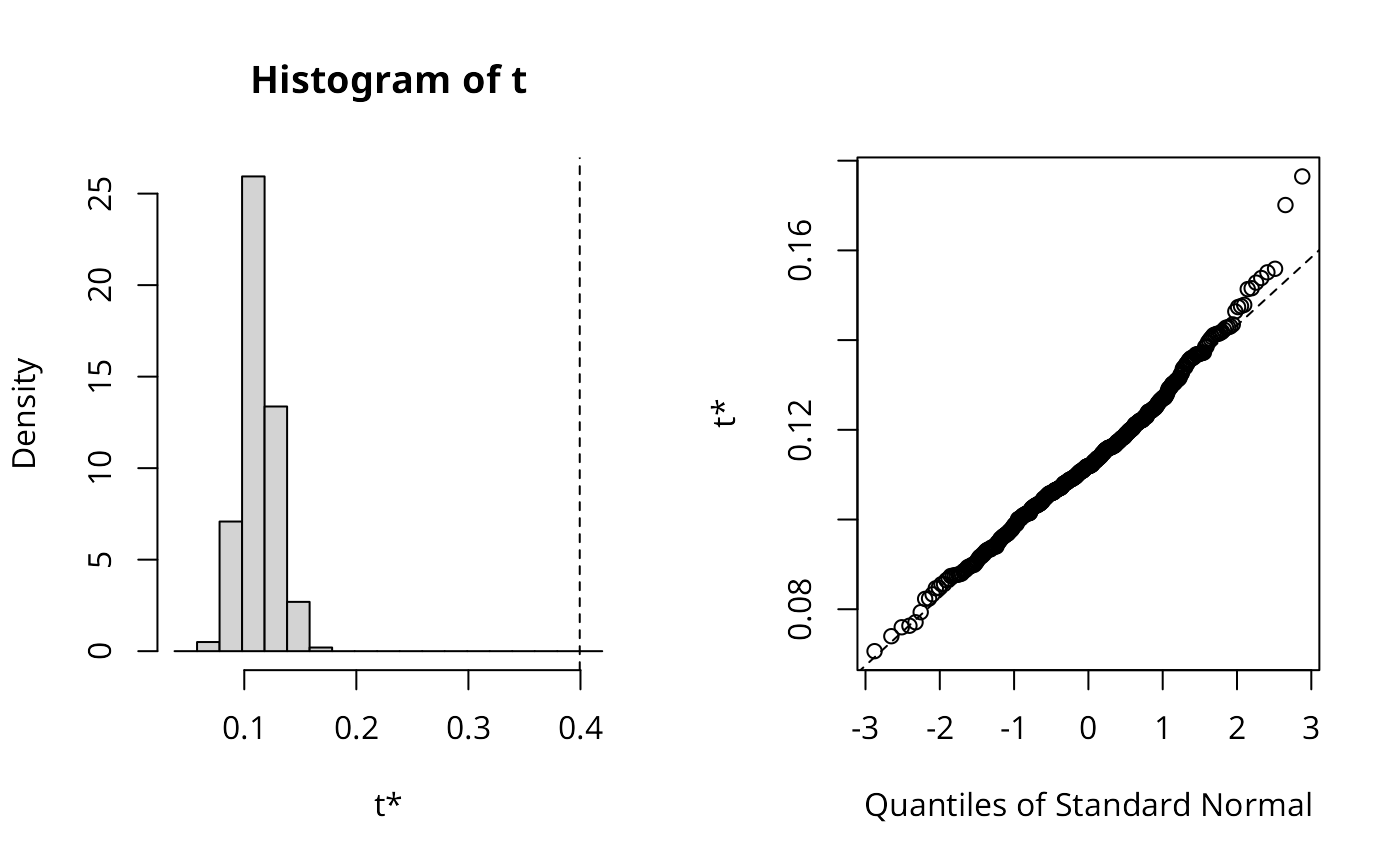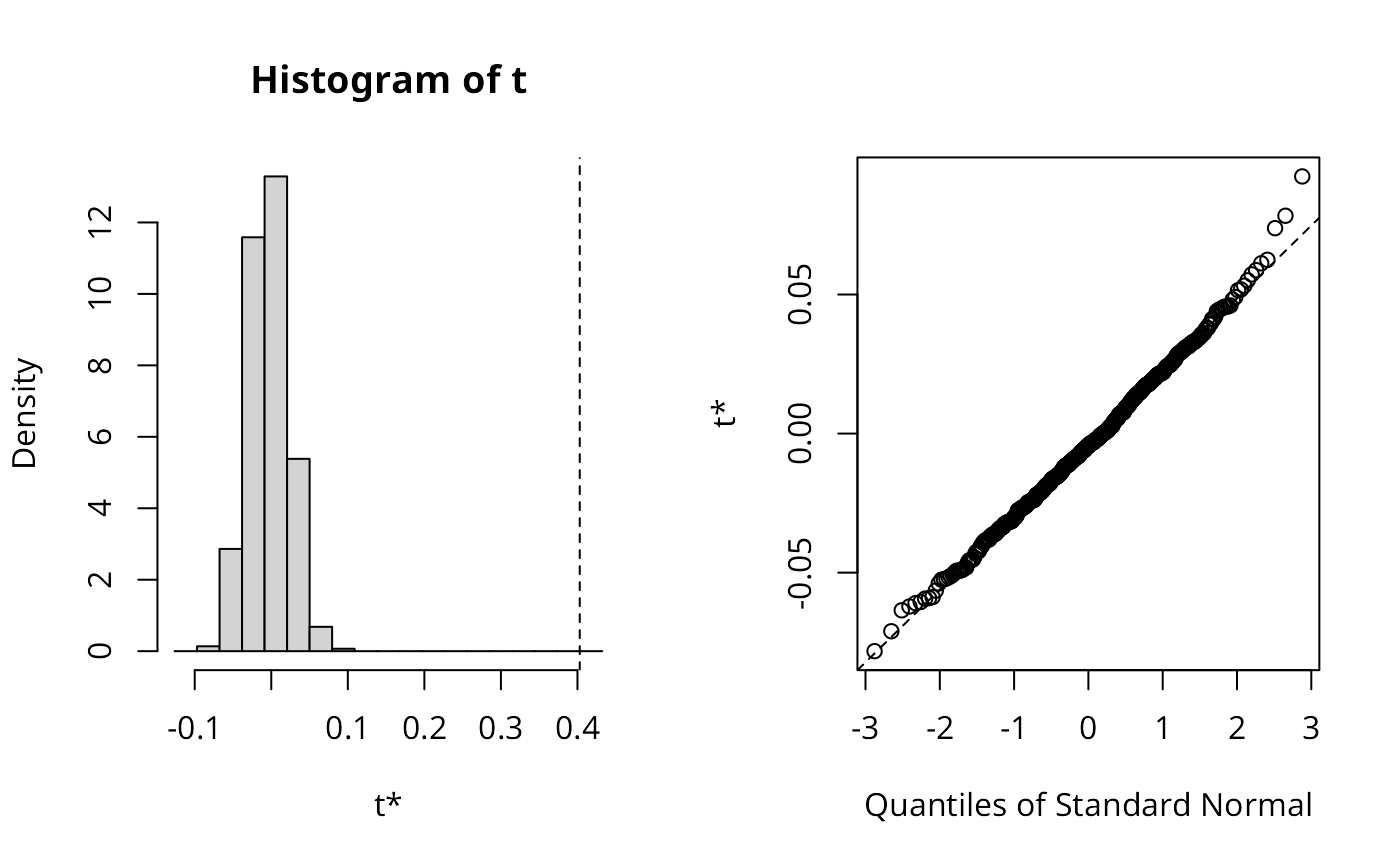set.seed(1)
lee_yx <- lee.mc(y, x, listw, nsim=499, return_boot=TRUE)
lee_yx$t0
#> [1] 0.3993476
boot::boot.ci(lee_yx, conf=c(0.99, 0.95, 0.9), type="basic")
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 499 bootstrap replicates
#> 
#> CALL : 
#> boot::boot.ci(boot.out = lee_yx, conf = c(0.99, 0.95, 0.9), type = "basic")
#> 
#> Intervals : 
#> Level      Basic         
#> 99%   ( 0.6363,  0.7236 )   
#> 95%   ( 0.6538,  0.7131 )   
#> 90%   ( 0.6584,  0.7098 )  
#> Calculations and Intervals on Original Scale
#> Some basic intervals may be unstable
plot(lee_yx)