Spatial 'K'luster Analysis by Tree Edge Removal

This function implements a SKATER procedure for spatial clustering analysis. This procedure essentialy begins with an edges set, a data set and a number of cuts. The output is an object of 'skater' class and is valid for input again.

Usage

skater(edges, data, ncuts, crit, vec.crit, method = c("euclidean", 
    "maximum", "manhattan", "canberra", "binary", "minkowski", 
    "mahalanobis"), p = 2, cov, inverted = FALSE)

Arguments

edges: A matrix with 2 colums with each row is an edge
data: A data.frame with data observed over nodes.
ncuts: The number of cuts
crit: A scalar or two dimensional vector with criteria for groups. Examples: limits of group size or limits of population size. If scalar, is the minimum criteria for groups.
vec.crit: A vector for evaluating criteria.
method: Character or function to declare distance method. If method is character, method must be "mahalanobis" or "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowisk". If method is one of "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowski", see dist for details, because this function as used to compute the distance. If method="mahalanobis", the mahalanobis distance is computed between neighbour areas. If method is a function, this function is used to compute the distance.
p: The power of the Minkowski distance.
cov: The covariance matrix used to compute the mahalanobis distance.
inverted: logical. If 'TRUE', 'cov' is supposed to contain the inverse of the covariance matrix.

Value

A object of skater class with:

groups: A vector with length equal the number of nodes. Each position identifies the group of node
edges.groups: A list of length equal the number of groups with each element is a set of edges
not.prune: A vector identifying the groups with are not candidates to partition.
candidates: A vector identifying the groups with are candidates to partition.
ssto: The total dissimilarity in each step of edge removal.

References

Assuncao, R.M., Lage J.P., and Reis, E.A. (2002). Analise de conglomerados espaciais via arvore geradora minima. Revista Brasileira de Estatistica, 62, 1-23.

Assuncao, R. M, Neves, M. C., Camara, G. and Freitas, C. da C. (2006). Efficient regionalization techniques for socio-economic geographical units using minimum spanning trees. International Journal of Geographical Information Science Vol. 20, No. 7, August 2006, 797-811

Author

Renato M. Assuncao and Elias T. Krainski

Examples

### loading data
GDAL37 <- numeric_version(unname(sf::sf_extSoftVersion()["GDAL"]), strict=FALSE)
(GDAL37 <- ifelse(is.na(GDAL37), FALSE, GDAL37 >= "3.7.0"))
#> [1] TRUE
file <- "etc/shapes/bhicv.gpkg.zip"
zipfile <- system.file(file, package="spdep")
if (GDAL37) {
    bh <- st_read(zipfile)
} else {
    td <- tempdir()
    bn <- sub(".zip", "", basename(file), fixed=TRUE)
    target <- unzip(zipfile, files=bn, exdir=td)
    bh <- st_read(target)
}
#> Reading layer `bhicv' from data source 
#>   `/tmp/Rtmp8nltTc/temp_libpath3e0f162c58ef7/spdep/etc/shapes/bhicv.gpkg.zip' 
#>   using driver `GPKG'
#> Simple feature collection with 98 features and 8 fields
#> Geometry type: POLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -45.02175 ymin: -20.93007 xmax: -42.50321 ymax: -18.08342
#> Geodetic CRS:  Corrego Alegre 1970-72
### data standardized 
dim(bh)
#> [1] 98  9
dpad <- data.frame(scale(as.data.frame(bh)[,5:8]))

### neighboorhod list
bh.nb <- poly2nb(bh)
bh.nb
#> Neighbour list object:
#> Number of regions: 98 
#> Number of nonzero links: 508 
#> Percentage nonzero weights: 5.289463 
#> Average number of links: 5.183673 

### calculating costs
lcosts <- nbcosts(bh.nb, dpad)
head(lcosts)
#> [[1]]
#>  [1] 1.5418355 2.5253558 1.4738620 1.8462822 1.7089412 1.5613667 1.0279919
#>  [8] 0.6334314 1.9029531 2.5816759
#> 
#> [[2]]
#> [1] 1.0847913 1.7723275 0.7940341
#> 
#> [[3]]
#> [1] 1.257984 2.634043 0.847224 1.807124
#> 
#> [[4]]
#> [1] 1.2579836 1.0548805 0.7862035
#> 
#> [[5]]
#> [1] 1.541835 1.295112 2.206320
#> 
#> [[6]]
#> [1] 0.9981915 1.3801441 1.5225548 1.3606678 0.9775650
#> 

### making listw
nb.w <- nb2listw(bh.nb, lcosts, style="B")
nb.w
#> Characteristics of weights list object:
#> Neighbour list object:
#> Number of regions: 98 
#> Number of nonzero links: 508 
#> Percentage nonzero weights: 5.289463 
#> Average number of links: 5.183673 
#> 
#> Weights style: B 
#> Weights constants summary:
#>    n   nn       S0       S1       S2
#> B 98 9604 1027.424 5192.868 55983.97

### find a minimum spanning tree
mst.bh <- mstree(nb.w,5)
str(mst.bh)
#>  'mst' num [1:97, 1:3] 5 12 13 13 11 31 39 40 31 40 ...

### the mstree plot
par(mar=c(0,0,0,0))
plot(st_geometry(bh), border=gray(.5))
pts <- st_coordinates(st_centroid(bh))
#> Warning: st_centroid assumes attributes are constant over geometries
plot(mst.bh, pts, col=2, 
     cex.lab=.6, cex.circles=0.035, fg="blue", add=TRUE)


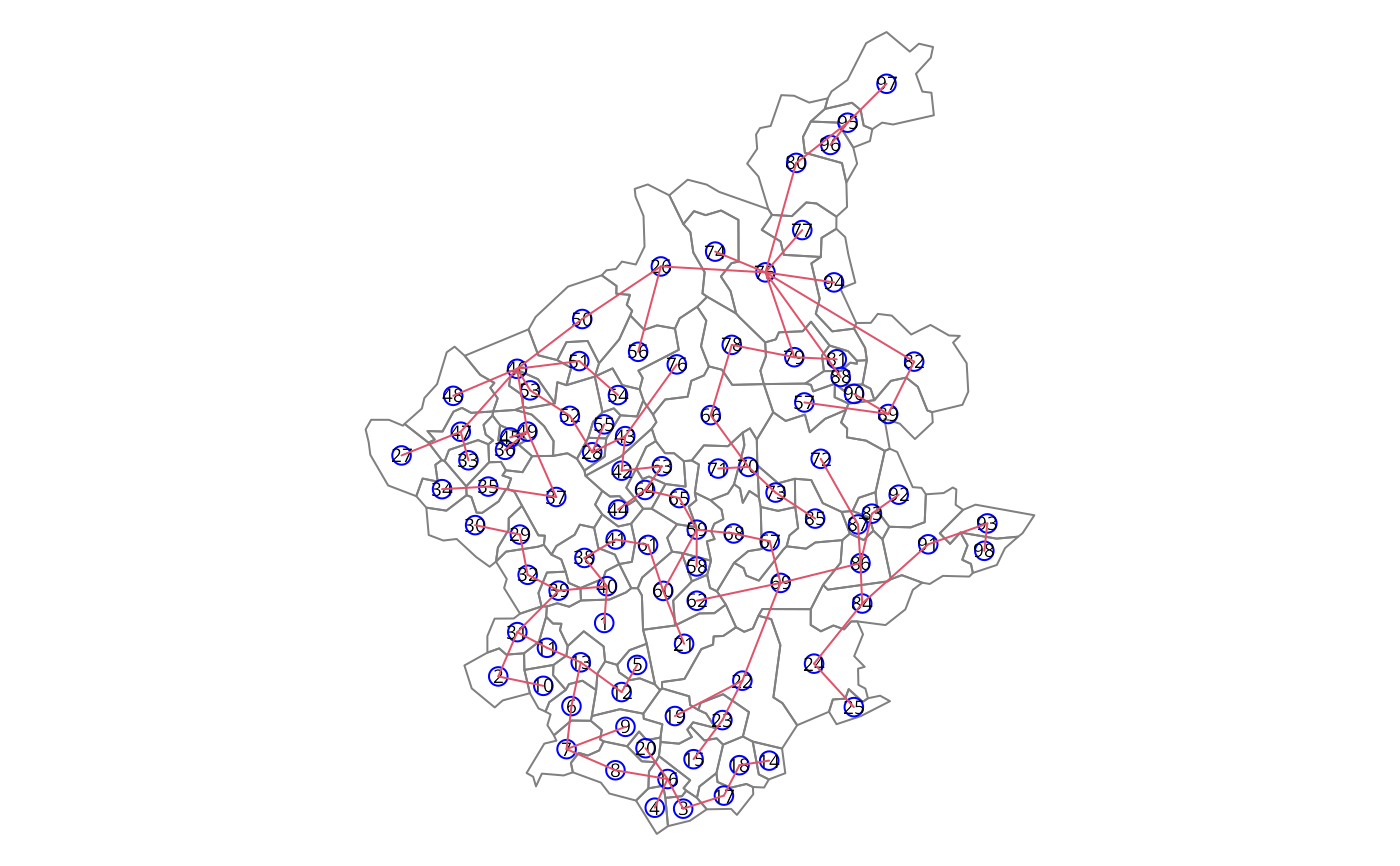### three groups with no restriction
res1 <- spdep::skater(edges=mst.bh[,1:2], data=dpad, ncuts=2)

### groups size
table(res1$groups)
#> 
#>  1  2  3 
#> 18 23 57 

### the skater plot
opar <- par(mar=c(0,0,0,0))
plot(res1, pts, cex.circles=0.035, cex.lab=.7)


### the skater plot, using other colors
plot(res1, pts, cex.circles=0.035, cex.lab=.7,
     groups.colors=heat.colors(length(res1$ed)))


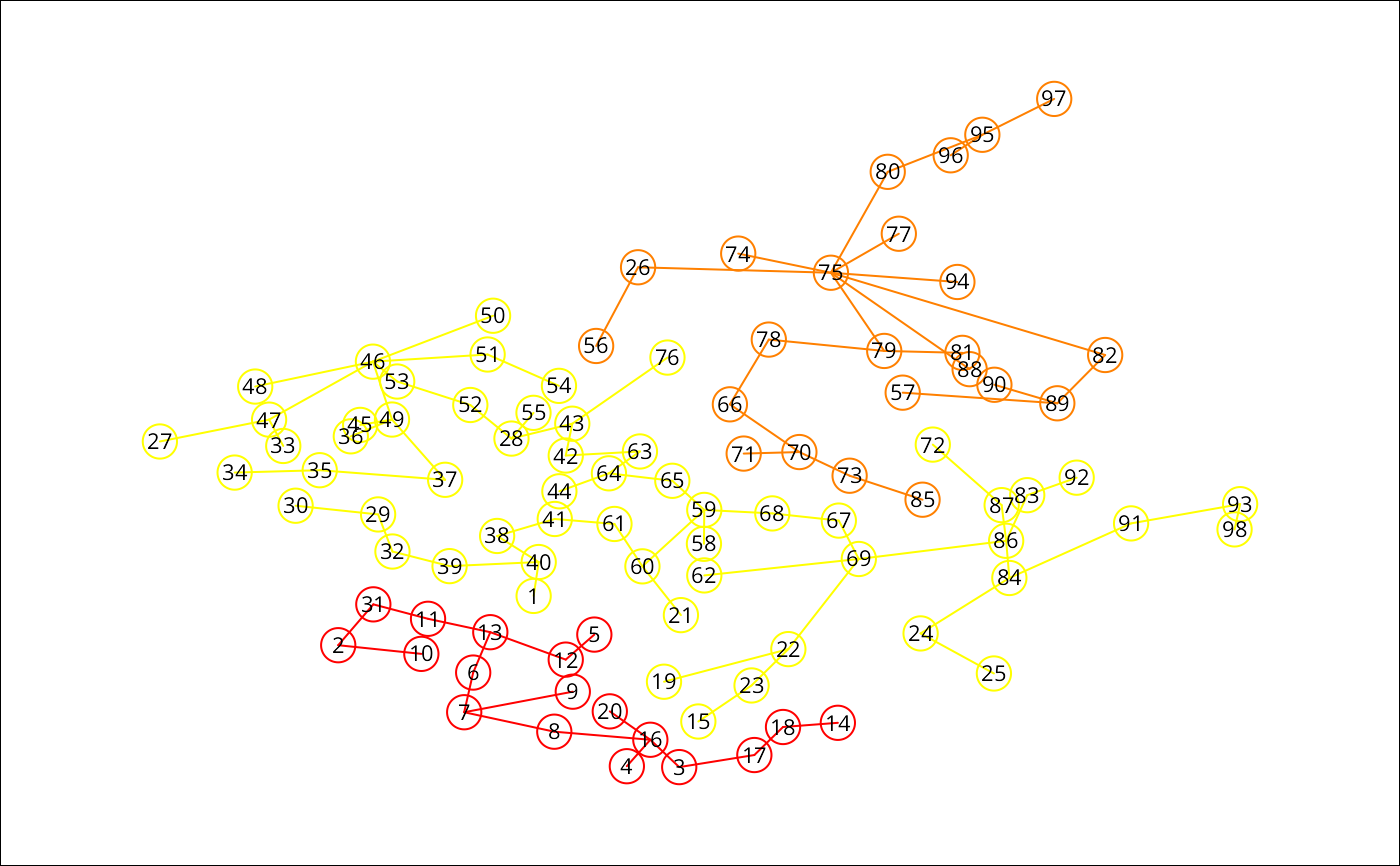### the Spatial Polygons plot
plot(st_geometry(bh), col=heat.colors(length(res1$edg))[res1$groups])


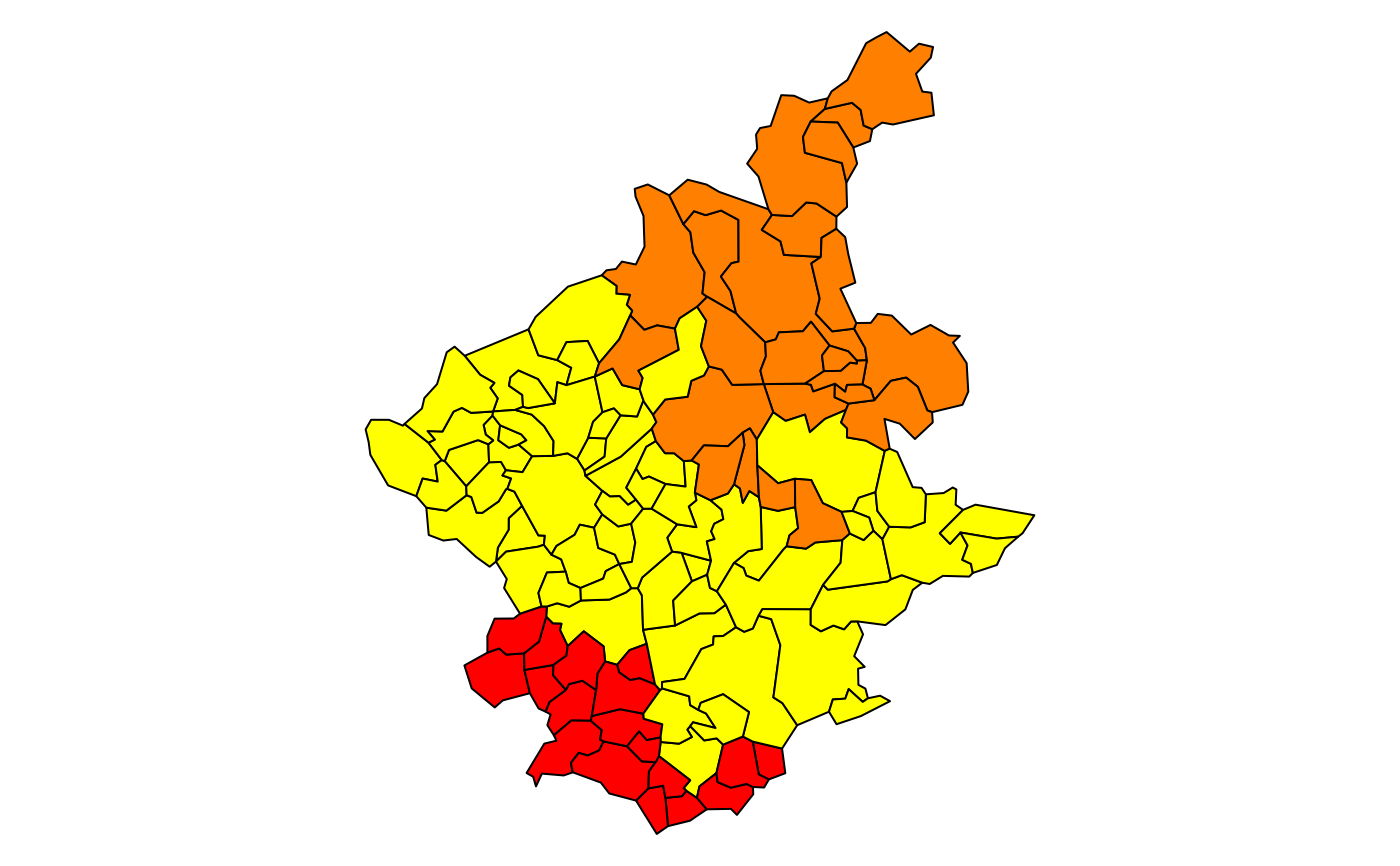#par(opar)
### EXPERT OPTIONS

### more one partition
res1b <- spdep::skater(res1, dpad, 1)

### length groups frequency
table(res1$groups)
#> 
#>  1  2  3 
#> 18 23 57 

table(res1b$groups)
#> 
#>  1  2  3  4 
#> 18 23 55  2 

### thee groups with minimum population 
res2 <- spdep::skater(mst.bh[,1:2], dpad, 2, 200000, bh$Pop)
table(res2$groups)
#> 
#>  1  2  3 
#> 22 37 39 

### thee groups with minimun number of areas
res3 <- spdep::skater(mst.bh[,1:2], dpad, 2, 3, rep(1,nrow(bh)))
table(res3$groups)
#> 
#>  1  2  3 
#> 18 23 57 

### thee groups with minimun and maximun number of areas
res4 <- spdep::skater(mst.bh[,1:2], dpad, 2, c(20,50), rep(1,nrow(bh)))
table(res4$groups)
#> 
#>  1  2  3 
#> 50 24 24 

### if I want to get groups with 20 to 40 elements
res5 <- spdep::skater(mst.bh[,1:2], dpad, 2,
   c(20,40), rep(1,nrow(bh))) ## DON'T MAKE DIVISIONS 
table(res5$groups)
#> 
#>  1 
#> 98 

### In this MST don't have groups with this restrictions
### In this case, first I do one division
### with the minimun criteria
res5a <- spdep::skater(mst.bh[,1:2], dpad, 1, 20, rep(1,nrow(bh))) 
table(res5a$groups)
#> 
#>  1  2 
#> 75 23 

### and do more one division with the full criteria
res5b <- spdep::skater(res5a, dpad, 1, c(20, 40), rep(1,nrow(bh)))
table(res5b$groups)
#> 
#>  1  2  3 
#> 22 23 53 

### and do more one division with the full criteria
res5c <- spdep::skater(res5b, dpad, 1, c(20, 40), rep(1,nrow(bh)))
table(res5c$groups)
#> 
#>  1  2  3  4 
#> 22 23 33 20 

### It don't have another divison with this criteria
res5d <- spdep::skater(res5c, dpad, 1, c(20, 40), rep(1,nrow(bh)))
table(res5d$groups)
#> 
#>  1  2  3  4 
#> 22 23 33 20 

# \dontrun{
data(boston, package="spData")
bh.nb <- boston.soi
dpad <- data.frame(scale(boston.c[,c(7:10)]))
### calculating costs
system.time(lcosts <- nbcosts(bh.nb, dpad))
#>    user  system elapsed 
#>   0.049   0.000   0.050 
### making listw
nb.w <- nb2listw(bh.nb, lcosts, style="B")
### find a minimum spanning tree
mst.bh <- mstree(nb.w,5)
### three groups with no restriction
system.time(res1 <- spdep::skater(mst.bh[,1:2], dpad, 2))
#>    user  system elapsed 
#>   1.646   0.110   1.763 
library(parallel)
nc <- max(2L, detectCores(logical=FALSE), na.rm = TRUE)-1L
# set nc to 1L here
if (nc > 1L) nc <- 1L
coresOpt <- get.coresOption()
invisible(set.coresOption(nc))
if(!get.mcOption()) {
# no-op, "snow" parallel calculation not available
  cl <- makeCluster(get.coresOption())
  set.ClusterOption(cl)
}
### calculating costs
system.time(plcosts <- nbcosts(bh.nb, dpad))
#>    user  system elapsed 
#>   0.047   0.001   0.047 
all.equal(lcosts, plcosts, check.attributes=FALSE)
#> [1] TRUE
### making listw
pnb.w <- nb2listw(bh.nb, plcosts, style="B")
### find a minimum spanning tree
pmst.bh <- mstree(pnb.w,5)
### three groups with no restriction
system.time(pres1 <- spdep::skater(pmst.bh[,1:2], dpad, 2))
#>    user  system elapsed 
#>   1.937   0.107   2.053 
if(!get.mcOption()) {
  set.ClusterOption(NULL)
  stopCluster(cl)
}
all.equal(res1, pres1, check.attributes=FALSE)
#> [1] TRUE
invisible(set.coresOption(coresOpt))
# }