Weighted Multivariate Spatial Autocorrelation Measures

The kernel-based weighted multivariate spatial autocorrelation measure delta proposed in Bavaud (2024) is implemented, together with support functions to create spatial weights matrices from symmetric binary adjacency matrices; summary and display methods are provided.

Usage

spatialdelta(dissimilarity_matrix, adjusted_spatial_weights,
 regional_weights=NULL, alternative = "greater")
# S3 method for class 'spatialdelta'
summary(object, ...)
# S3 method for class 'summary.spatialdelta'
print(x, digits=getOption("digits"), ...)
linearised_diffusive_weights(adjacency_matrix, regional_weights, t_choice = 2)
metropolis_hastings_weights(adjacency_matrix, regional_weights)
iterative_proportional_fitting_weights(adjacency_matrix, regional_weights,
 g=0.001, iter=1000, tol=1e-10, tol.margins=1e-10, print=FALSE)
graph_distance_weights(adjacency_matrix, regional_weights, c=NULL)
# S3 method for class 'adjusted_spatial_weights'
as.matrix(x, ...)
plot_spatialcoords(x, ...)
# Default S3 method
plot_spatialcoords(x, ...)
# S3 method for class 'spatialdelta'
plot_spatialcoords(x, cols = c(1L, 2L),
 mult = c(1, 1), power = 1L, fmult = NULL, names = attr(x, "rnames"), bg = 1,
 pos = 3, cex = 0.6, largest = NULL, ...)
plot_moran(x, y, ...)
# Default S3 method
plot_moran(x, y, ...)
# S3 method for class 'spatialdelta'
plot_moran(x, y, fmult = NULL, names = attr(x, "rnames"),
 bg = 1, pos = 3, cex = 0.6, largest = NULL, ...)
plot_spatialscree(x, ...)
# Default S3 method
plot_spatialscree(x, ...)
# S3 method for class 'spatialdelta'
plot_spatialscree(x, lwd=2, ...)
factorial_coordinates(x)
# Default S3 method
factorial_coordinates(x)
# S3 method for class 'spatialdelta'
factorial_coordinates(x)
plot_factorialcoords(x, ...)
# Default S3 method
plot_factorialcoords(x, ...)
# S3 method for class 'spatialdelta'
plot_factorialcoords(x, cols = c(1L, 2L),
 mult = c(1, 1), fmult = NULL, names = attr(x, "rnames"), bg = 1, pos = 3,
 cex = 0.6, largest = NULL, ...)
plot_factorialscree(x, ...)
# Default S3 method
plot_factorialscree(x, ...)
# S3 method for class 'spatialdelta'
plot_factorialscree(x, ...)
localdelta(x, ...)
# Default S3 method
localdelta(x, ...)
# S3 method for class 'spatialdelta'
localdelta(x, names = attr(x, "rnames"), ...)
cornish_fisher(x, ...)
# Default S3 method
cornish_fisher(x, ...)
# S3 method for class 'spatialdelta'
cornish_fisher(x, ...)

Arguments

dissimilarity_matrix: dissimilarity_matrix is a square matrix of dissimilarities between (possibly multivariate) observations
adjusted_spatial_weights: adjusted_spatial_weights is a square matrix of spatial weights as returned by construction functions linearised_diffusive_weights, metropolis_hastings_weights, iterative_proportional_fitting_weights, graph_distance_weights or similar; only the named construction functions pass regional_weights through to spatialdelta, so for matrices constructed in other ways, this argument is required
regional_weights: default NULL, regional_weights are weights reflecting the contribution of each observation to the (possibly multivariate) data set, they may be uniform, but none can be zero, and they must sum to unity; if adjusted_spatial_weights is an "adjusted_spatial_weights" object created by linearised_diffusive_weights, metropolis_hastings_weights, iterative_proportional_fitting_weights or graph_distance_weights, regional_weights is passed as an attribute
alternative: a character string specifying the alternative hypothesis, must be one of "greater" (default), "less" or "two.sided"
object, x: object, x are objects returned by spatialdelta of class "spatialdelta", or of class "adjusted_spatial_weights"
digits: default getOption("digits"), or a non-null value specifying the minimum number of significant digits to be printed in values
adjacency_matrix: adjacency_matrix is a symmetric binary adjacency matrix
t_choice: default 2, the inverse of the largest eigenvalue of the adjusted Laplacian adjacency matrix (t2, Bavaud 2024, page 583), otherwise 1 (t1, page 579)
g: default 0.001, (Bavaud 2024, page 579, 589), a small quantity to lift binary adjacency matrix above zero
iter, tol, tol.margins, print: arguments passed to Ipfp
c: default NULL, a coefficient greater than zero and less than or equal to -1/min(B) where B is the matrix of scalar products associated with the distance matrix; if not given, -1/min(B) is used
y: a numeric vector from which to create a Moran plot
cols: integer vector of length 2, default c(1L, 2L), giving the two columns of the regional or factorial coordinates to plot
mult: numeric vector of length 2, default c(1, 1), to scale or reverse axes as signs are not given to be the same for different eigenproblem implementations
power: integer vector of length 1, default 1; if higher, use a powered kernel
fmult: default NULL for automatic scaling of the circle symbols expressing the observation weights f in the plot as (0.02*diff(range(X)))/diff(range(regional_weights)) where X is the first vector of coordinates; may be set manually to a numeric value
names: default attr(x, "rnames"), the coordinates will be annotated with these strings passed through from the "region.id" attribute of the "nb" object used to create the adjusted_spatial_weights matrix from the "adjacency_matrix" object as row and column names
bg, pos, cex, lwd: arguments passed to graphics functions or methods
largest: default NULL, may be integer > 0 and <= the region count, permitting names to be plotted only for the largest circle symbols
...: other arguments passed to other functions or methods

Details

In general, the user should choose one of the functions for constructing spatial weights from the symmetric binary, or similar to symmetric - for example row-standardised - adjacency matrix. The cornish_fisher method updates the standard deviate and p-value if the pair of skewness and excess kurtosis estimates are within the required domain.

Value

spatialdelta returns an object with classes "spatialdelta" and "htest". Its print method treats it as an "htest" object. Other methods use additional attributes:

Kx: Multivariate kernel matrix eq. 16
Kw: Spatial weights kernel matrix eq. 21
regional_weights: Input observation weights
adjusted_spatial_weights: Input spatial adjusted_spatial_weightseights
B: symmetric matrix of scalar products eq. 15
VI: Spatial component of delta variance
Vx: Multivariate component of delta variance
Vd0: Variance of delta calculated in another way eq. 38
alphamu: Spatial component of delta skewness
alphalambda: Multivariate component of delta skewness
gammamu: Spatial component of delta excess kurtosis
gammalambda: Multivariate component of delta excess kurtosis
rnames: Region names passed through from row/column names of adjusted_spatial_weights, from the "region.id" attribute of the "nb" object used to create the adjusted_spatial_weights matrix from the "adjacency_matrix" object

linearised_diffusive_weights, metropolis_hastings_weights, iterative_proportional_fitting_weights and graph_distance_weights return square spatial weights matrices (the latter two return matrices created by metropolis_hastings_weights if igraph or mipfp are not available); factorial_coordinates returns a square factorial matrix; localdelta returns a vector of local deltas eq. 30.

References

Bavaud, F. (2024), Measuring and Testing Multivariate Spatial Autocorrelation in a Weighted Setting: A Kernel Approach. Geographical Analysis, 56: 573-599. doi:10.1111/gean.12390 ; Bivand, R. (2025) Implementing a weighted measure of multivariate spatial autocorrelation, Cahiers Du Centre De Linguistique Et Des Sciences Du Langage, (69), 19-35, doi:10.26034/la.cdclsl.2025.8343

Author

Roger Bivand, Roger.Bivand@nhh.no

Note

The input adjacency matrix should be symmetric, and not have sub-graphs or islands - it should be possible to step across graph edges from any observation to any other.

Examples

toy_f <- c(0.4, 0.1, 0.3, 0.2)
toy_xa <- c(4, 9, 1, 1)
toy_nba <- structure(list(c(2L, 3L, 4L), c(1L), c(1L, 4L), c(1L, 3L)),
 class="nb", region.id=as.character(1:4))
toy_gla <- list(c(0.25, 0.5, 0.25), c(1), c(2/3, 1/3), c(0.5, 0.5))
toy_wa <- nb2mat(toy_nba, glist=toy_gla, style="W")
spatialdelta(dissimilarity_matrix=as.matrix(dist(toy_xa))^2,
 adjusted_spatial_weights=toy_wa, regional_weights=toy_f, alternative="two.sided")
#> 
#> 	Bavaud delta normal approximation
#> 
#> data:  as.matrix(dist(toy_xa))^2 
#> weights: toy_wa
#> Standard deviate = 1.9799, p-value = 0.04771
#> alternative hypothesis: two.sided
#> sample estimates:
#>           delta     Expectation        Variance        Skewness Excess Kurtosis 
#>      0.13333333     -0.33333333      0.05555556      0.16162441             Inf 
#> 
toy_xb <- toy_xa
toy_glb <- list(c(0.5, 0.125, 0.25, 0.125), c(0.5, 0.5), c(1/3, 0.5, 1/6), c(0.25, 0.25, 0.5))
toy_nbb <- include.self(toy_nba)
toy_wb <- nb2mat(toy_nbb, glist=toy_glb, style="W")
spatialdelta(dissimilarity_matrix=as.matrix(dist(toy_xb))^2,
 adjusted_spatial_weights=toy_wb, regional_weights=toy_f, alternative="two.sided")
#> 
#> 	Bavaud delta normal approximation
#> 
#> data:  as.matrix(dist(toy_xb))^2 
#> weights: toy_wb
#> Standard deviate = 1.9799, p-value = 0.04771
#> alternative hypothesis: two.sided
#> sample estimates:
#>           delta     Expectation        Variance        Skewness Excess Kurtosis 
#>      0.56666667      0.33333333      0.01388889      0.16162441             Inf 
#> 
toy_xc <- c(3, 3, 1, 1)
toy_nbc <- structure(list(c(3L, 4L), c(3L, 4L), c(1L, 2L), c(1L, 2L)),
 class="nb", region.id=as.character(1:4))
toy_glc <- list(c(0.6, 0.4), c(0.6, 0.4), c(0.8, 0.2), c(0.8, 0.2))
toy_wc <- nb2mat(toy_nbc, glist=toy_glc, style="W")
spatialdelta(dissimilarity_matrix=as.matrix(dist(toy_xc))^2,
 adjusted_spatial_weights=toy_wc, regional_weights=toy_f, alternative="two.sided")
#> 
#> 	Bavaud delta normal approximation
#> 
#> data:  as.matrix(dist(toy_xc))^2 
#> weights: toy_wc
#> Standard deviate = -2.2361, p-value = 0.02535
#> alternative hypothesis: two.sided
#> sample estimates:
#>           delta     Expectation        Variance        Skewness Excess Kurtosis 
#>     -1.00000000     -0.33333333      0.08888889     -0.63887656             Inf 
#> 
# \donttest{
if (require(Guerry, quietly=TRUE)) {
data(gfrance85)
gfrance85 <- st_as_sf(gfrance85)
moral <- scale(st_drop_geometry(gfrance85)[, 7:12])
Dmoral <- as.matrix(dist(moral))^2
fG <- gfrance85$Pop1831/sum(gfrance85$Pop1831)
gnb <- poly2nb(gfrance85, row.names=gfrance85$Department)
frG <- nb2mat(gnb, style="B")
ldwG <- linearised_diffusive_weights(adjacency_matrix=frG, regional_weights=fG)
mhwG <- metropolis_hastings_weights(adjacency_matrix=frG, regional_weights=fG)
ifwG <- iterative_proportional_fitting_weights(adjacency_matrix=frG, regional_weights=fG)
gdwG <- graph_distance_weights(adjacency_matrix=frG, regional_weights=fG)
(moral_ldw <- spatialdelta(dissimilarity_matrix=Dmoral, adjusted_spatial_weights=ldwG))
(cornish_fisher(moral_ldw))
moral_mhw <- spatialdelta(dissimilarity_matrix=Dmoral, adjusted_spatial_weights=mhwG)
moral_ifw <- spatialdelta(dissimilarity_matrix=Dmoral, adjusted_spatial_weights=ifwG)
moral_gdw <- spatialdelta(dissimilarity_matrix=Dmoral, adjusted_spatial_weights=gdwG)
opar <- par(mfrow=c(2, 2))
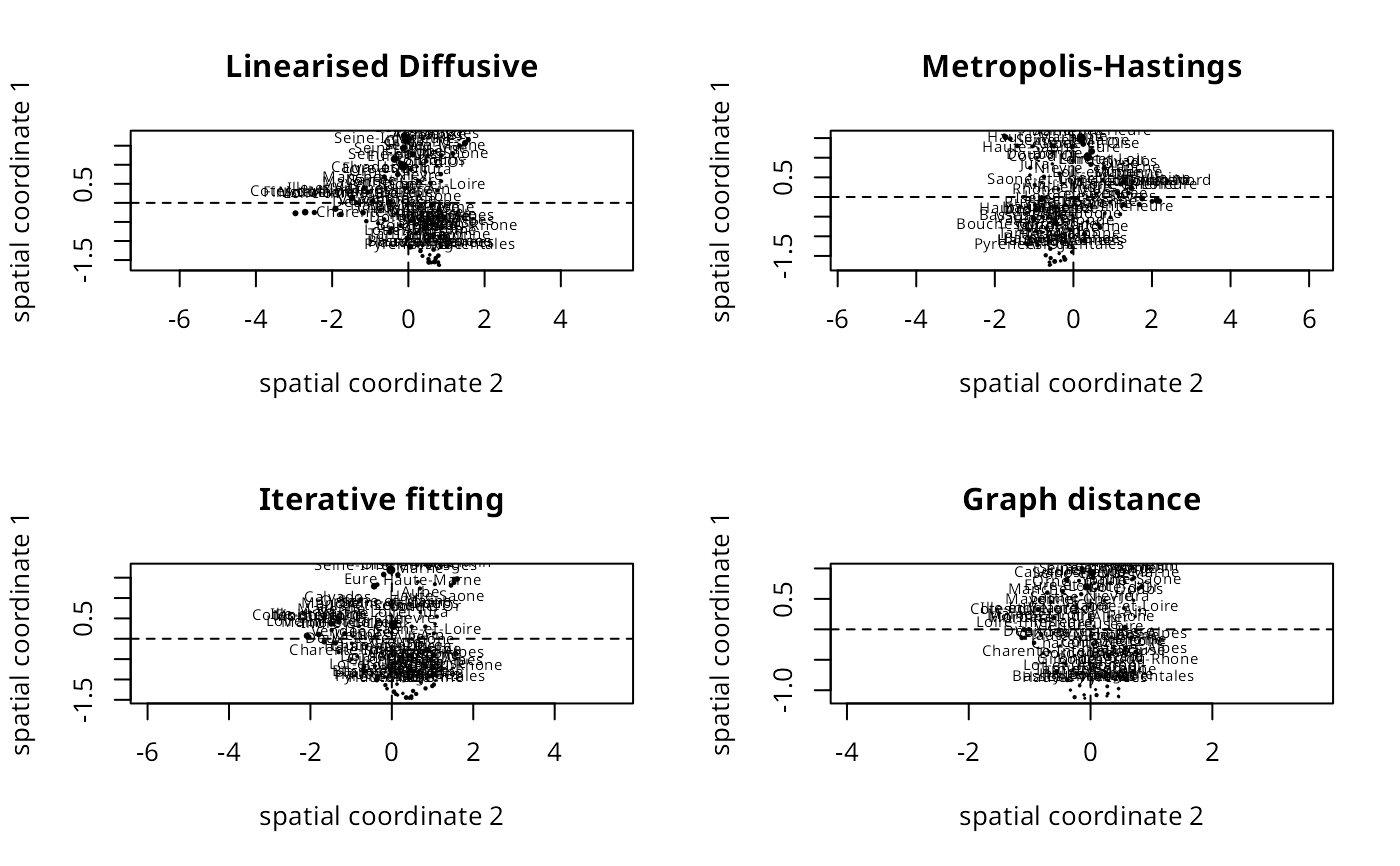
plot_spatialcoords(moral_ldw, cols=c(2,1), mult=c(-1, -1), main="Linearised Diffusive", asp=1)
plot_spatialcoords(moral_mhw, cols=c(2,1), mult=c(1, 1), main="Metropolis-Hastings", asp=1)
plot_spatialcoords(moral_ifw, cols=c(2,1), mult=c(1, 1), main="Iterative fitting", asp=1)
plot_spatialcoords(moral_gdw, cols=c(2,1), mult=c(1, 1), main="Graph distance", asp=1)
par(opar)
opar <- par(mfrow=c(2, 2))
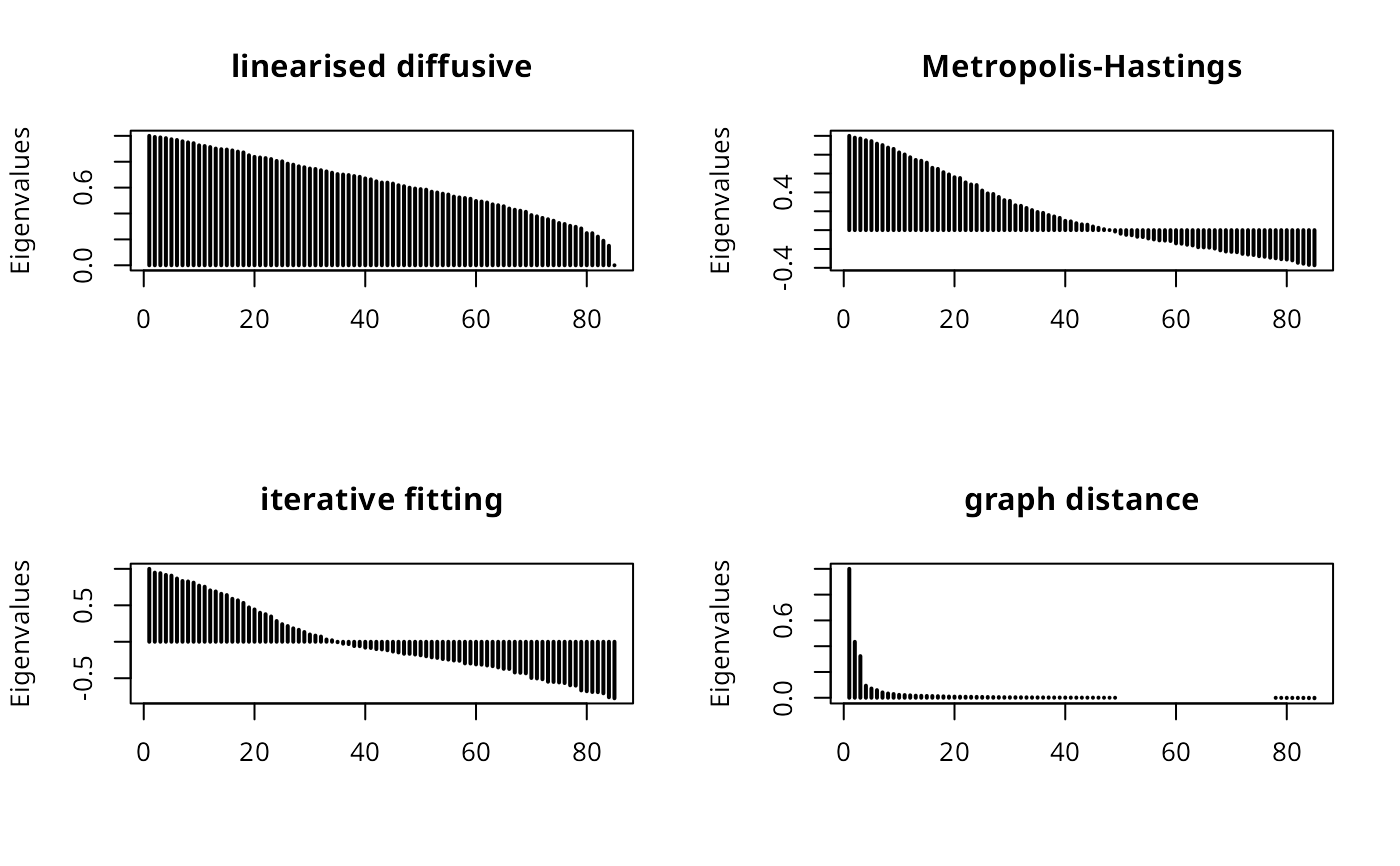
plot_spatialscree(moral_ldw, main="linearised diffusive")
plot_spatialscree(moral_mhw, main="Metropolis-Hastings")
plot_spatialscree(moral_ifw, main="iterative fitting")
plot_spatialscree(moral_gdw, main="graph distance")
par(opar)
Crime_pers <- scale(gfrance85$Crime_pers)
funif <- rep(1/length(Crime_pers), length(Crime_pers))
lw <- nb2listw(gnb, style="W")
Crime_pers_delta <- spatialdelta(dissimilarity_matrix=as.matrix(dist(Crime_pers))^2,
 adjusted_spatial_weights=listw2mat(lw), regional_weights=funif)
Crime_pers_delta$estimate["delta"]
locdelta <- localdelta(Crime_pers_delta)
moran.test(Crime_pers, lw, randomisation=FALSE)$estimate["Moran I statistic"]
locmoran <- localmoran(c(Crime_pers), lw)[,1]
all.equal(locmoran, locdelta) 
all.equal(unname(moral_ldw$estimate["delta"]), # Eq. 30 p. 588
 sum(fG * localdelta(moral_ldw)))
all.equal(unname(moral_mhw$estimate["delta"]), # Eq. 30 p. 588
 sum(fG * localdelta(moral_mhw)))
all.equal(unname(moral_ifw$estimate["delta"]), # Eq. 30 p. 588
 sum(fG * localdelta(moral_ifw)))
all.equal(unname(moral_gdw$estimate["delta"]), # Eq. 30 p. 588
 sum(fG * localdelta(moral_gdw)))
}


#> [1] TRUE
# }