7. Spherical geometry in sf using s2geometry

Introduction

This vignette describes what spherical geometry implies, and how package sf uses the s2geometry library (http://s2geometry.io) for geometrical measures, predicates and transformations.
After sf has been loaded, it will report whether s2 is being used; it can be switched off (resorting to flat space geometry) by sf_use_s2(FALSE).

library(sf)
## Linking to GEOS 3.10.2, GDAL 3.4.1, PROJ 8.2.1; sf_use_s2() is TRUE
## 
## Attaching package: 'sf'
## The following objects are masked from 'package:lwgeom':
## 
##     st_minimum_bounding_circle, st_perimeter

library(s2)

Most of the package’s functions start with s2_ in the same way that most sf function names start with st_. Most sf functions automatically use s2 functions when working with ellipsoidal coordinates; if this is not the case, e.g. for st_voronoi(), a warning like

Warning message:
In st_voronoi.sfc(st_geometry(x), st_sfc(envelope), dTolerance,  :
  st_voronoi does not correctly triangulate longitude/latitude data

is emitted.

Projected and geographic coordinates

Spatial coordinates either refer to projected (or Cartesian) coordinates, meaning that they are associated to points on a flat space, or to unprojected or geographic coordinates, when they refer to angles (latitude, longitude) pointing to locations on a sphere (or ellipsoid). The flat space is also referred to as $R^2$ , the sphere as $S^2$

Package sf implements simple features, a standard for point, line, and polygon geometries where geometries are built from points (nodes) connected by straight lines (edges). The simple feature standard does not say much about its suitability for dealing with geographic coordinates, but the topological relational system it builds upon (DE9-IM) refer to $R^2$ , the two-dimensional flat space.

Yet, more and more data are routinely served or exchanged using geographic coordinates. Using software that assumes an $R^2$ , flat space may work for some problems, and although sf up to version 0.9-x had some functions in place for spherical/ellipsoidal computations (from package lwgeom, for computing area, length, distance, and for segmentizing), it has also happily warned the user that it is doing $R^2$ , flat computations with such coordinates with messages like

although coordinates are longitude/latitude, st_intersects assumes that they are planar

hinting to the responsibility of the user to take care of potential problems. Doing this however leaves ambiguities, e.g. whether LINESTRING(-179 0,179 0)

passes through POINT(0 0), or
passes through POINT(180 0)

and whether it is

a straight line, cutting through the Earth’s surface, or
a curved line following the Earth’s surface

Starting with sf version 1.0, if you provide a spatial object in a geographical coordinate reference system, sf uses the new package s2 (Dunnington, Pebesma, Rubak 2020) for spherical geometry, which has functions for computing pretty much all measures, predicates and transformations on the sphere. This means:

no more hodge-podge of some functions working on $R^2$ , with annoying messages, some on the ellipsoid
a considerable speed increase for some functions
no computations on the ellipsoid (which are considered more accurate, but are also slower)

The s2 package is really a wrapper around the C++ s2geometry library which was written by Google, and which is used in many of its products (e.g. Google Maps, Google Earth Engine, Bigquery GIS) and has been translated in several other programming languages.

With projected coordinates sf continues to work in $R^2$ as before.

Fundamental differences

Compared to geometry on $R^2$ , and DE9-IM, the s2 package brings a few fundamentally new concepts, which are discussed first.

Polygons on $S^2$ divide the sphere in two parts

On the sphere ( $S^2$ ), any polygon defines two areas; when following the exterior ring, we need to define what is inside, and the definition is the left side of the enclosing edges. This also means that we can flip a polygon (by inverting the edge order) to obtain the other part of the globe, and that in addition to an empty polygon (the empty set) we can have the full polygon (the entire globe).

Simple feature geometries should obey a ring direction too: exterior rings should be counter clockwise, interior (hole) rings should be clockwise, but in some sense this is obsolete as the difference between exterior ring and interior rings is defined by their position (exterior, followed by zero or more interior). sf::read_sf() has an argument check_ring_dir that checks, and corrects, ring directions and many (legacy) datasets have wrong ring directions. With wrong ring directions, many things still work.

For $S^2$ , ring direction is essential. For that reason, st_as_s2 has an argument oriented = FALSE, which will check and correct ring directions, assuming that all exterior rings occupy an area smaller than half the globe:

nc = read_sf(system.file("gpkg/nc.gpkg", package="sf")) # wrong ring directions
s2_area(st_as_s2(nc, oriented = FALSE)[1:3]) # corrects ring direction, correct area:
## [1] 1137107793  610916077 1423145355
s2_area(st_as_s2(nc, oriented = TRUE)[1:3]) # wrong direction: Earth's surface minus area
## [1] 5.100649e+14 5.100655e+14 5.100646e+14
nc = read_sf(system.file("gpkg/nc.gpkg", package="sf"), check_ring_dir = TRUE)
s2_area(st_as_s2(nc, oriented = TRUE)[1:3]) # no second correction needed here:
## [1] 1137107793  610916077 1423145355

The default conversion from sf to s2 uses oriented = FALSE, so that we get

all(units::drop_units(st_area(nc)) == s2_area(st_as_s2(nc, oriented = FALSE)))
## [1] TRUE

Here is an example where the oceans are computed as the difference from the full polygon representing the entire globe,

g = st_as_sfc("POLYGON FULL", crs = 'EPSG:4326')
g
## Geometry set for 1 feature 
## Geometry type: POLYGON
## Dimension:     XY
## Bounding box:  xmin: -180 ymin: -90 xmax: 180 ymax: 90
## Geodetic CRS:  WGS 84
## POLYGON FULL

and the countries, and shown in an orthographic projection:

options(s2_oriented = TRUE) # don't change orientation from here on
co = st_as_sf(s2_data_countries())
oc = st_difference(g, st_union(co)) # oceans
b = st_buffer(st_as_sfc("POINT(-30 52)", crs = 'EPSG:4326'), 9800000) # visible half
i = st_intersection(b, oc) # visible ocean
plot(st_transform(i, "+proj=ortho +lat_0=52 +lon_0=-30"), col = 'blue')

(Note that the printing of POLYGON FULL is not valid WKT according to the simple feature standard, which does not include this.)

We can now calculate the proportion of the Earth’s surface covered by oceans:

st_area(oc) / st_area(g)
## 0.711301 [1]

Semi-open polygon boundaries

Polygons in s2geometry can be

CLOSED: they contain their boundaries, and a point on the boundary intersects with the polygon
OPEN: they do not contain their boundaries, points on the boundary do not intersect with the polygon
SEMI-OPEN: they contain part of their boundaries, but no boundary of non-overlapping polygons is contained by more than one polygon.

In principle the DE9-IM model deals with interior, boundary and exterior, and intersection predicates are sensitive to this (the difference between contains and covers is all about boundaries). DE9-IM however cannot uniquely assign points to polygons when polygons form a polygon coverage (no overlaps, but shared boundaries). This means that if we would count points by polygon, and some points fall on shared polygon boundaries, we either miss them (contains) or we count them double (covers, intersects); this might lead to bias and require post-processing. Using SEMI-OPEN non-overlapping polygons guarantees that every point is assigned to maximally one polygon in an intersection. This corresponds to e.g. how this would be handled in a grid (raster) coverage, where every grid cell (typically) only contains its upper-left corner and its upper and left sides.

a = st_as_sfc("POINT(0 0)", crs = 'EPSG:4326')
b = st_as_sfc("POLYGON((0 0,1 0,1 1,0 1,0 0))", crs = 'EPSG:4326')
st_intersects(a, b, model = "open")
## Sparse geometry binary predicate list of length 1, where the predicate
## was `intersects'
##  1: (empty)
st_intersects(a, b, model = "closed")
## Sparse geometry binary predicate list of length 1, where the predicate
## was `intersects'
##  1: 1
st_intersects(a, b, model = "semi-open") # a toss
## Sparse geometry binary predicate list of length 1, where the predicate
## was `intersects'
##  1: (empty)
st_intersects(a, b) # default: closed
## Sparse geometry binary predicate list of length 1, where the predicate
## was `intersects'
##  1: 1

Bounding cap, bounding rectangle

Computing the minimum and maximum values over coordinate ranges, as sf does with st_bbox(), is of limited value for spherical coordinates because due the the spherical space, the area covered is not necessarily covered by the coordinate range. Two examples:

small regions covering the antimeridian (longitude +/- 180) end up with a huge longitude range, which doesn’t make clear the antimeridian is spanned
regions including a pole will end up with a latitude range not extending to +/- 90

S2 has two alternatives: the bounding cap and the bounding rectangle:

fiji = s2_data_countries("Fiji")
aa = s2_data_countries("Antarctica")
s2_bounds_cap(fiji)
##        lng       lat    angle
## 1 178.7459 -17.15444 1.801369
s2_bounds_rect(c(fiji,aa))
##     lng_lo    lat_lo    lng_hi    lat_hi
## 1  177.285 -18.28799 -179.7933 -16.02088
## 2 -180.000 -90.00000  180.0000 -63.27066

The cap reports a bounding cap (circle) as a mid point (lat, lng) and an angle around this point. The bounding rectangle reports the _lo and _hi bounds of lat and lng coordinates. Note that for Fiji, lng_lo being higher than lng_hi indicates that the region covers (crosses) the antimeridian.

Switching between S2 and GEOS

The two-dimensional $R^2$ library that was formerly used by sf is GEOS, and sf can be instrumented to use GEOS or s2. First we will ask if s2 is being used by default:

sf_use_s2()
## [1] TRUE

then we can switch it off (and use GEOS) by

sf_use_s2(FALSE)
## Spherical geometry (s2) switched off

and switch it on (and use s2) by

sf_use_s2(TRUE)
## Spherical geometry (s2) switched on

Measures

Area

options(s2_oriented = FALSE) # correct orientation from here on
library(sf)
library(units)
## udunits database from /usr/share/xml/udunits/udunits2.xml
nc = read_sf(system.file("gpkg/nc.gpkg", package="sf"))
sf_use_s2(TRUE)
a1 = st_area(nc)
sf_use_s2(FALSE)
## Spherical geometry (s2) switched off
a2 = st_area(nc)
plot(a1, a2)
abline(0, 1)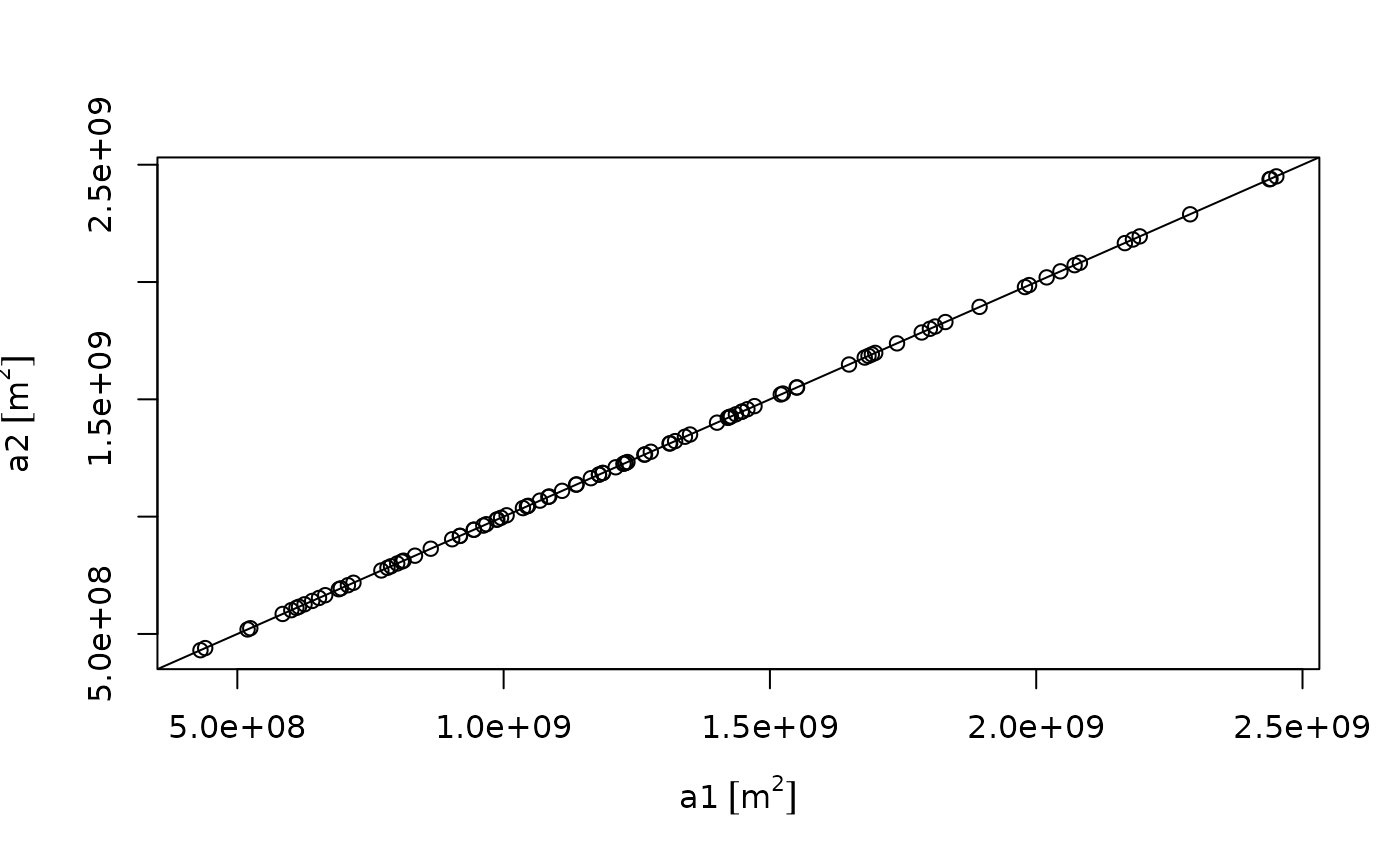

summary((a1 - a2)/a1)
##       Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
## -2.638e-04 -1.650e-04 -7.133e-05 -6.448e-05  1.598e-05  2.817e-04

Length

nc_ls = st_cast(nc, "MULTILINESTRING")
sf_use_s2(TRUE)
## Spherical geometry (s2) switched on
l1 = st_length(nc_ls)
sf_use_s2(FALSE)
## Spherical geometry (s2) switched off
l2 = st_length(nc_ls)
plot(l1 , l2)
abline(0, 1)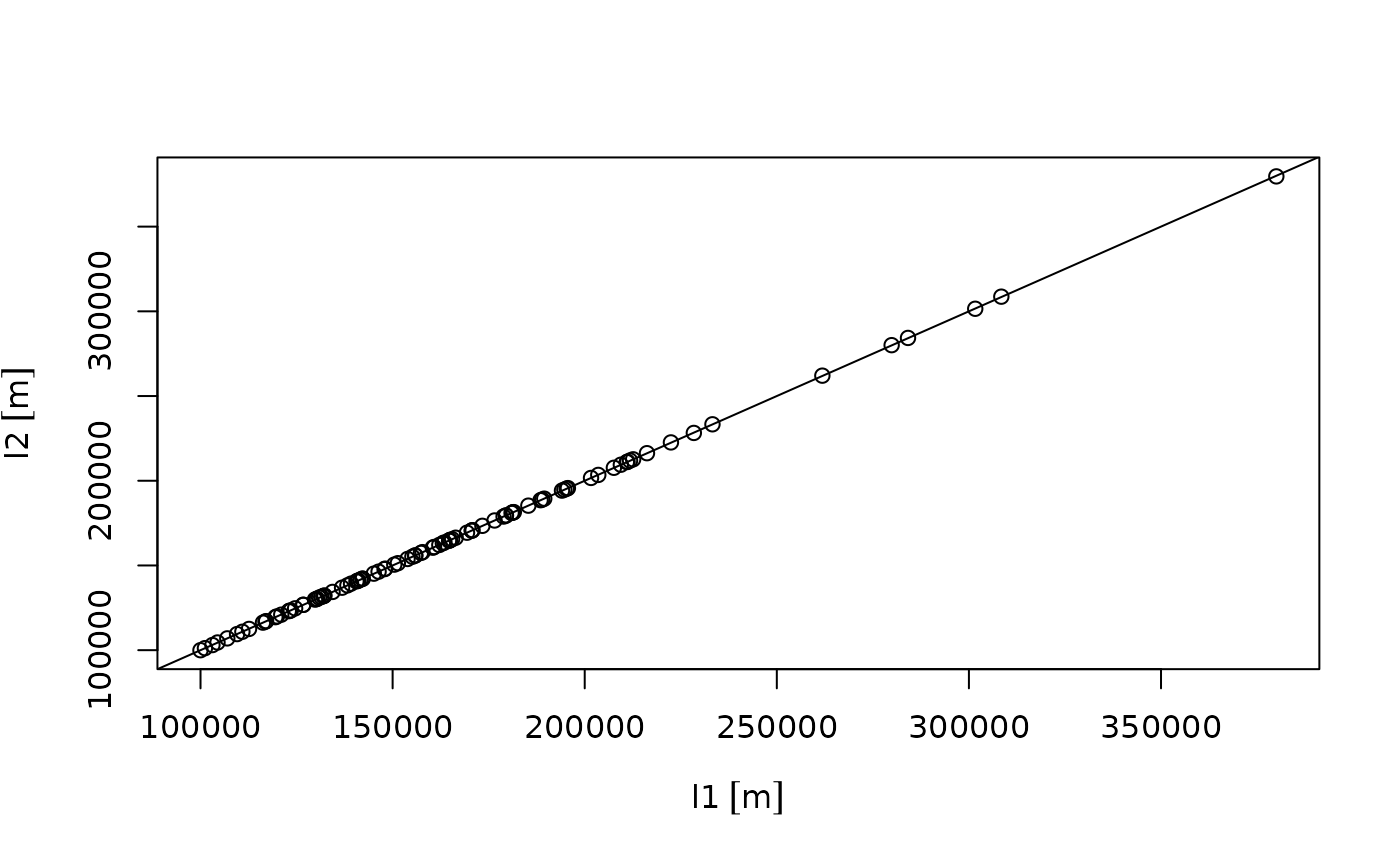

summary((l1-l2)/l1)
##       Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
## -0.0012301 -0.0004396 -0.0001258 -0.0001123  0.0001742  0.0009660

Distances

sf_use_s2(TRUE)
## Spherical geometry (s2) switched on
d1 = st_distance(nc, nc[1:10,])
sf_use_s2(FALSE)
## Spherical geometry (s2) switched off
d2 = st_distance(nc, nc[1:10,])
plot(as.vector(d1), as.vector(d2))
abline(0, 1)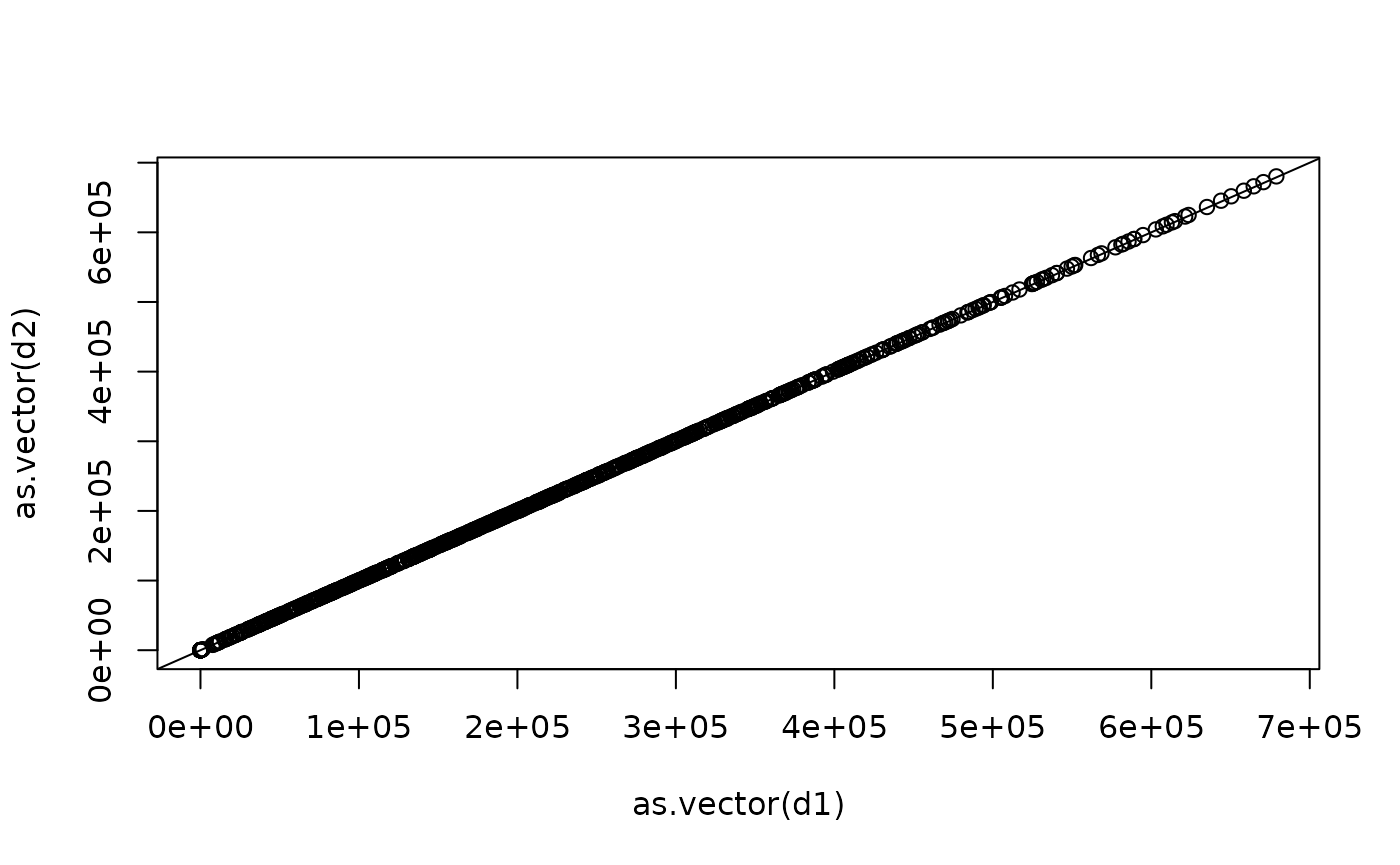

summary(as.vector(d1)-as.vector(d2))
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -1424.5  -613.2  -236.5  -319.5     0.0   460.1

Predicates

All unary and binary predicates are available in s2, except for st_relate() with a pattern. In addition, when using the s2 predicates, depending on the model, intersections with neighbours are only reported when model is closed (the default):

sf_use_s2(TRUE)
## Spherical geometry (s2) switched on
st_intersects(nc[1:3,], nc[1:3,]) # self-intersections + neighbours
## Sparse geometry binary predicate list of length 3, where the predicate
## was `intersects'
##  1: 1, 2
##  2: 1, 2, 3
##  3: 2, 3
sf_use_s2(TRUE)
st_intersects(nc[1:3,], nc[1:3,], model = "semi-open") # only self-intersections
## Sparse geometry binary predicate list of length 3, where the predicate
## was `intersects'
##  1: 1
##  2: 2
##  3: 3

Transformations

st_intersection(), st_union(), st_difference(), and st_sym_difference() are available as s2 equivalents. N-ary intersection and difference are not (yet) present; cascaded union is present; unioning by feature does not work with s2.

Buffers

Buffers can be calculated for features with geographic coordinates as follows, using an unprojected object representing the UK as an example:

uk = s2_data_countries("United Kingdom")
class(uk)
## [1] "s2_geography" "wk_vctr"
uk_sfc = st_as_sfc(uk) 
uk_buffer = st_buffer(uk_sfc, dist = 20000)
uk_buffer2 = st_buffer(uk_sfc, dist = 20000, max_cells = 10000)
uk_buffer3 = st_buffer(uk_sfc, dist = 20000, max_cells = 100)
class(uk_buffer)
## [1] "sfc_MULTIPOLYGON" "sfc"
plot(uk_sfc)
plot(uk_buffer)
plot(uk_buffer2)
plot(uk_buffer3)
uk_sf = st_as_sf(uk)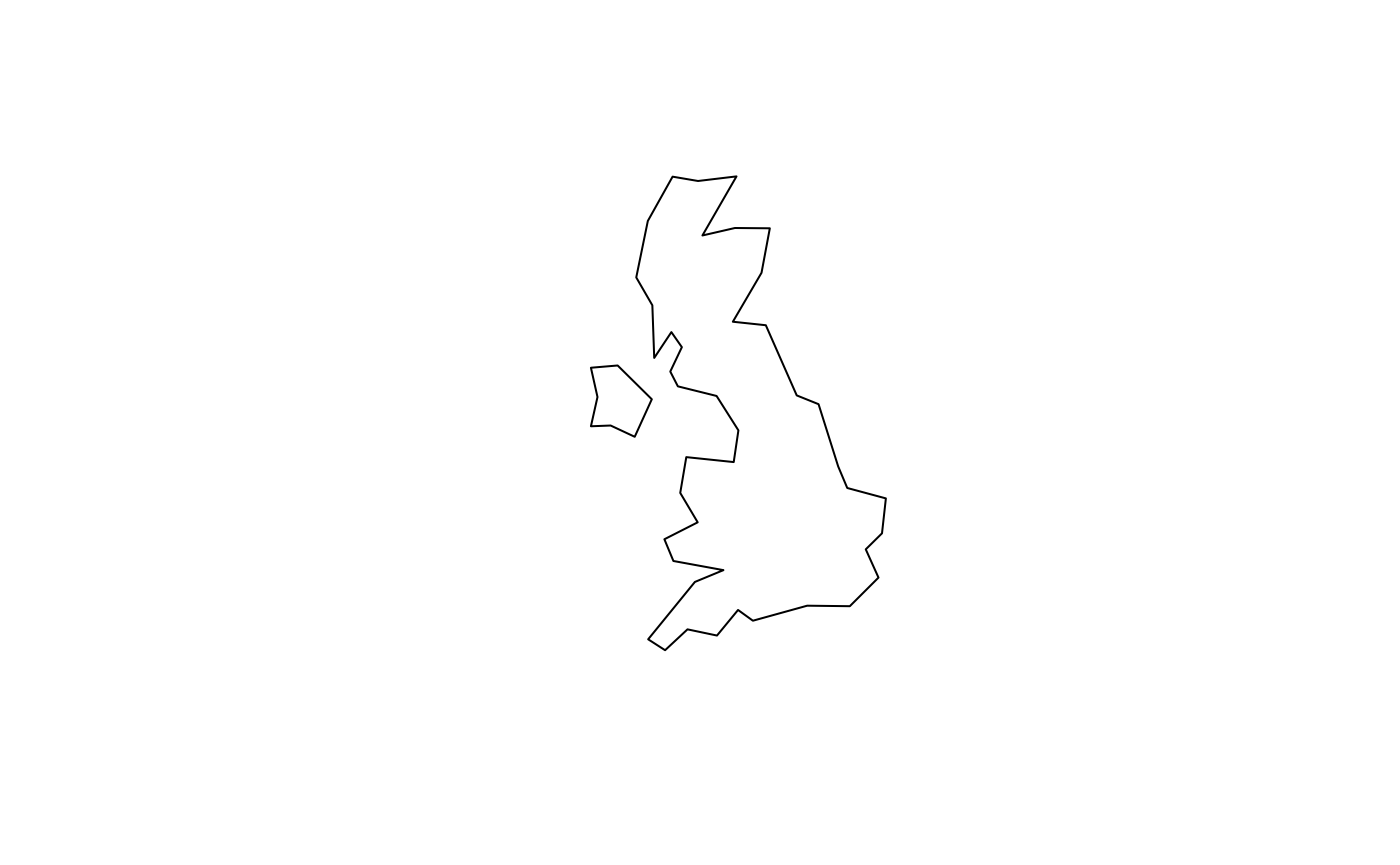

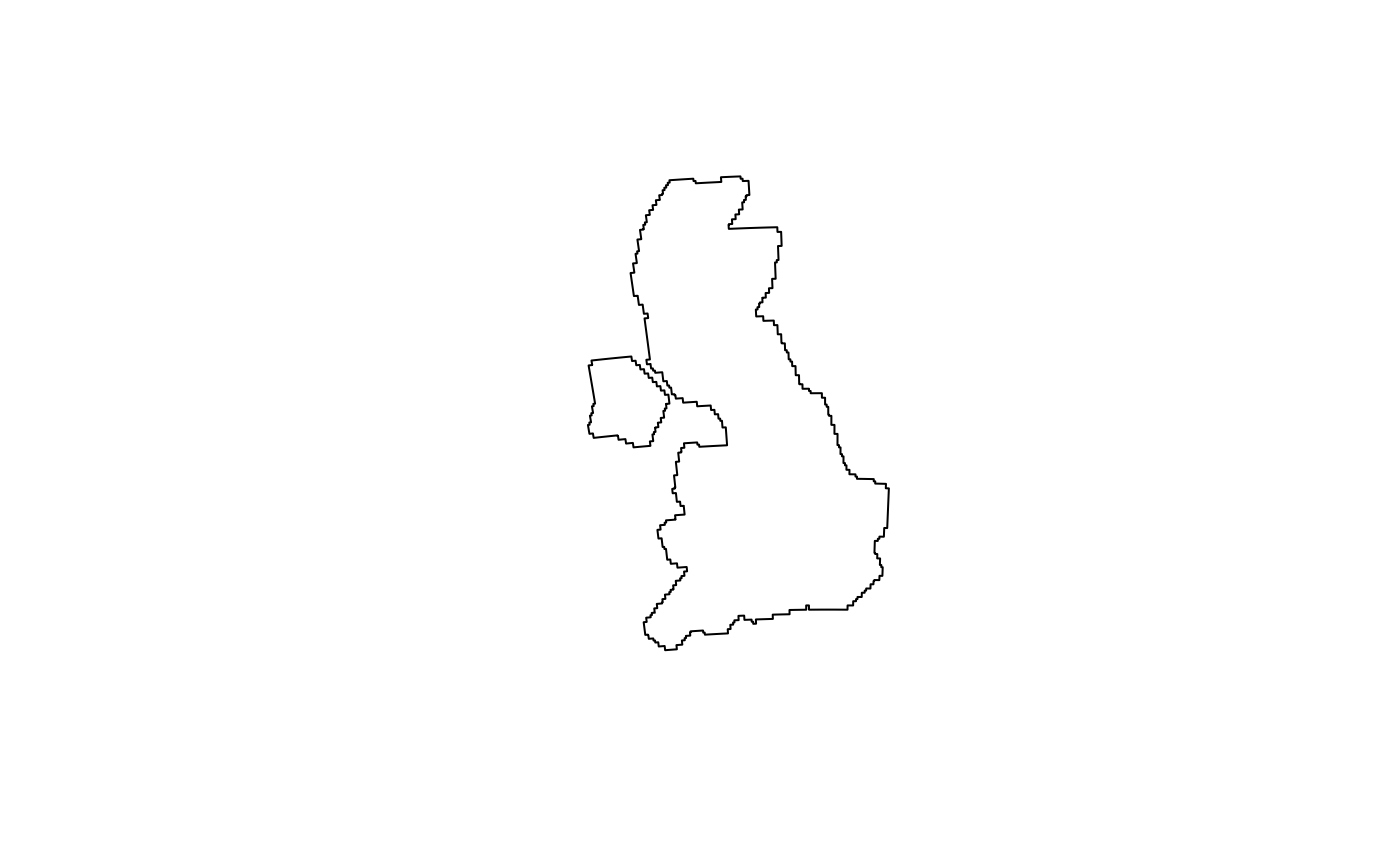
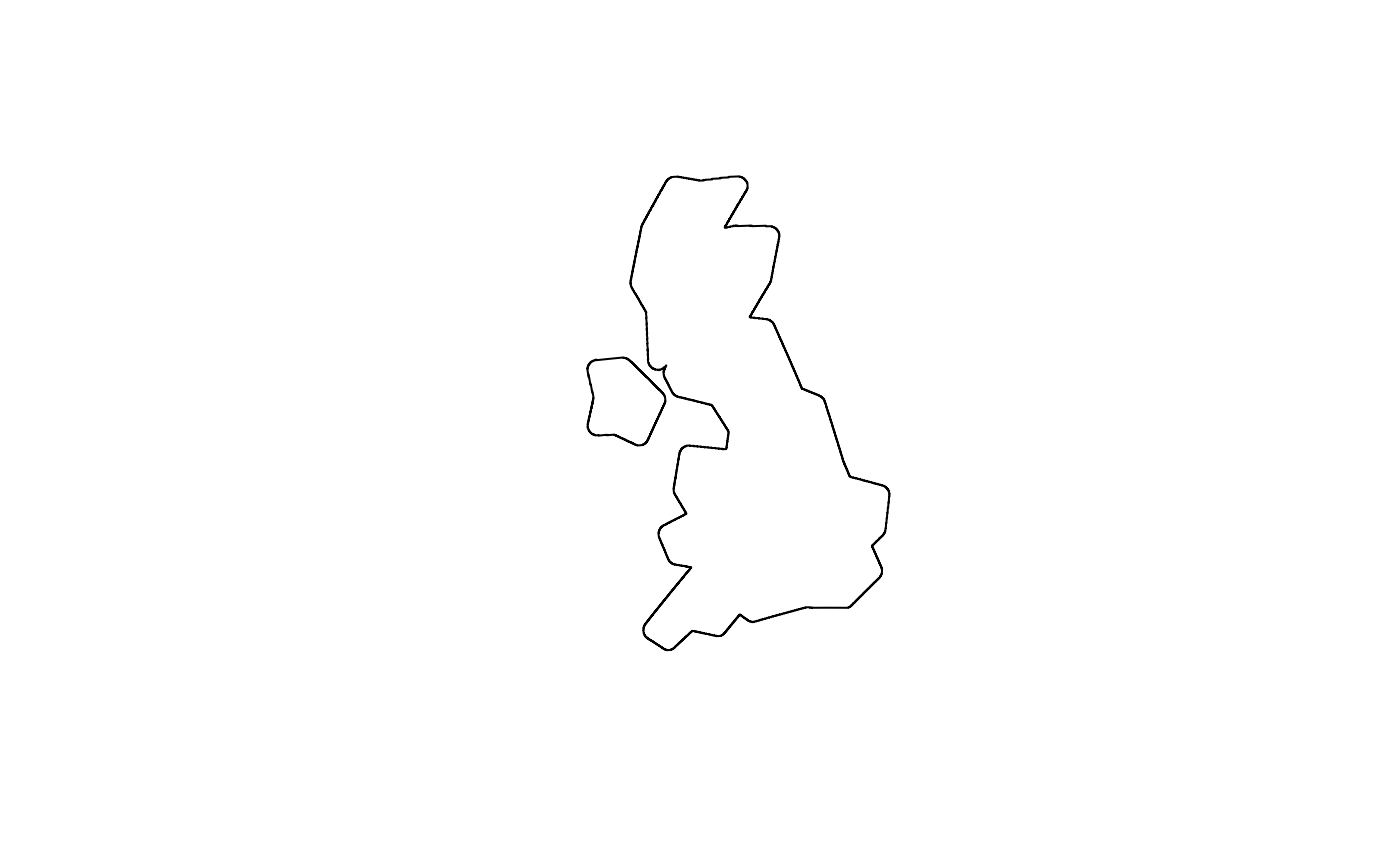
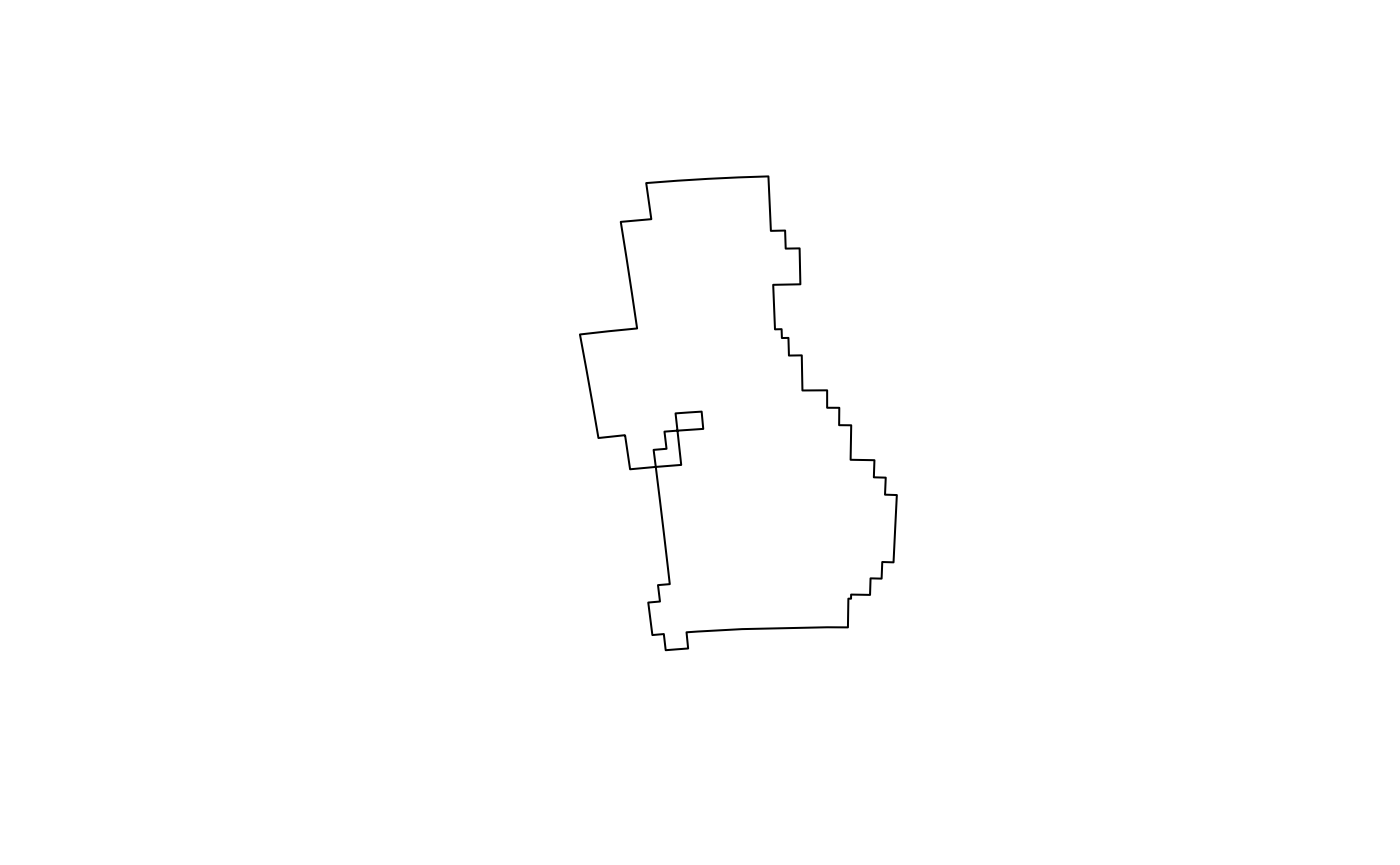
The plots above show that you can adjust the level of spatial precision in the results of s2 buffer operations with the max_cells argument, set to 1000 by default. Deciding on an appropriate value is a balance between excessive detail increasing computational resources (represented by uk_buffer2, bottom left) and excessive simplification (bottom right). Note that buffers created with s2 always follow s2 cell boundaries, they are never smooth. Hence, choosing a large number for max_cells leads to seemingly smooth but, zoomed in, very complex buffers.

To achieve a similar result you could first transform the result and then use sf::st_buffer(). A simple benchmark shows the computational efficiency of the s2 geometry engine in comparison with transforming and then creating buffers:

# the sf way
system.time({
  uk_projected = st_transform(uk_sfc, 27700)
  uk_buffer_sf = st_buffer(uk_projected, dist = 20000)
})
##    user  system elapsed 
##   0.023   0.000   0.023
# sf way with few than the 30 segments in the buffer
system.time({
  uk_projected = st_transform(uk_sfc, 27700)
  uk_buffer_sf2 = st_buffer(uk_projected, dist = 20000, nQuadSegs = 4)
})
##    user  system elapsed 
##   0.009   0.000   0.009
# s2 with default cell size
system.time({
  uk_buffer = s2_buffer_cells(uk, distance = 20000)
})
##    user  system elapsed 
##    0.03    0.00    0.03
# s2 with 10000 cells
system.time({
  uk_buffer2 = s2_buffer_cells(uk, distance = 20000, max_cells = 10000)
})
##    user  system elapsed 
##   0.283   0.000   0.283
# s2 with 100 cells
system.time({
  uk_buffer2 = s2_buffer_cells(uk, distance = 20000, max_cells = 100)
})
##    user  system elapsed 
##   0.004   0.000   0.003

The result of the previous benchmarks emphasizes the point that there are trade-offs between geographic resolution and computational resources, something that web developers working on geographic services such as Google Maps understand well. In this case the default setting of 1000 cells, which runs slightly faster than the default transform -> buffer workflow, is probably appropriate given the low resolution of the input geometry representing the UK.

`st_buffer` or `st_is_within_distance`?

As discussed in the sf issue tracker, deciding on workflows and selecting appropriate levels of level of geographic resolution can be an iterative process. st_buffer() as powered by GEOS, for $R^2$ data, are smooth and (nearly) exact. st_buffer() as powered by $S^2$ is rougher, complex, non-smooth, and may need tuning. An common pattern where st_buffer() is used is this:

compute buffers around a set of features x (points, lines, polygons)
within each of these buffers, find all occurrences of some other spatial variable y and aggregate them (e.g. count points, or average a raster variable like precipitation or population density)
work with these aggregated values (discard the buffer)

When this is the case, and you are working with geographic coordinates, it may pay off to not compute buffers, but instead directly work with st_is_within_distance() to select, for each feature of x, all features of y that are within a certain distance d from x. The $S^2$ version of this function uses spatial indexes, so is fast for large datasets.

References

Dewey Dunnington, Edzer Pebesma and Ege Rubak, 2020. s2: Spherical Geometry Operators Using the $S^2$ Geometry Library. https://r-spatial.github.io/s2/, https://github.com/r-spatial/s2

Edzer Pebesma and Dewey Dunnington